Существенной характеристикой числа является понятие его абсолютной величины – модуля. Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это слово, имеющее множество значений, применяется не только в математике, но и в физике, архитектуре, технике, программировании и других точных науках.
Несмотря на кажущуюся простоту определения модуля числа, решение уравнений и неравенств, содержащих неизвестные под знаком модуля, вызывает определенные трудности. По-видимому, они связаны с тем, что решение задач подобного рода предполагает элементарные навыки исследования, логического мышления, заключающиеся в переборе различных возможных вариантов, так как в подавляющем большинстве задач одно уравнение или неравенство с модулем равносильно совокупности или системе нескольких уравнений и неравенств, освобожденных от знака модуля.
В этой главе мы систематизировали информацию о модуле и рассмотрели некоторые методы решения уравнений и неравенств с модулем.
|
|
|
Модулем числа называют расстояние от начала отсчета до точки, изображающей это число на числовой оси.
Модуль числа 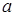 обозначают символом
обозначают символом 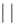 .
.
Другими словами, геометрически 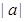 означает расстояние на числовой оси от начала отсчета до точки, изображающей число
означает расстояние на числовой оси от начала отсчета до точки, изображающей число 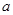 .
.
Если 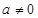 , то на числовой оси существует две точки
, то на числовой оси существует две точки 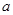 и
и 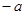 , равноудаленной от нуля, модули которых равны.
, равноудаленной от нуля, модули которых равны.
Если 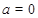 , то на числовой оси
, то на числовой оси 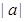 изображают точкой
изображают точкой 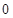 .
.
Пример. Решим уравнение: 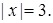
Решение. Согласно геометрической интерпретации модуля, уравнение описывает множество точек, удаленных от начала отсчета на расстояние 3. Это точки 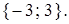
Ответ. –3; 3.
Пример. Решим уравнение: 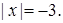
Решение. Согласно геометрической интерпретации модуля, расстояние не может быть отрицательно. Следовательно, данное уравнение решений не имеет.
Ответ. Решений нет.
Термин «модуль» ввел английский математик Р. Котес (1682 – 1716), знак модуля немецкий математик К. Вейерштрасс (1815-1897) в 1841 г.
Иногда вместо термина «модуль» используют термин «абсолютная величина» или «абсолютное значение» числа.
Дадим алгебраическое определение модуля.
Определение. Модуль числа 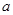 или абсолютная величина числа
или абсолютная величина числа 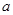 равна
равна 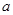 , если
, если 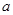 больше или равно нулю и равна
больше или равно нулю и равна 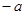 , если
, если 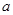 меньше нуля:
меньше нуля:
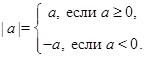
Пример. В соответствии с приведенным определением 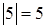 ,
, 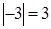 ,
, 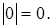
Из определения модуля следует, что для любого действительного числа 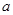 ,
, 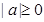 .
.
Пример. Решим уравнение: 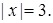
Решение. Согласно алгебраическому определению модуля, имеем: 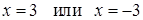 .
.
Ответ. –3; 3.
Пример. Решим уравнение: 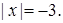
Решение. Согласно алгебраическому определению модуля, имеем: 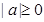 . Следовательно, данное уравнение решений не имеет.
. Следовательно, данное уравнение решений не имеет.
Ответ. Решений нет.
Теорема 6. Абсолютная величина действительного числа 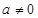 равна большему из двух чисел
равна большему из двух чисел 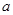 или
или 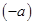 .
.
|
|
|
Доказательство. Если число 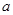 положительно, то число
положительно, то число 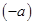 отрицательно, то есть
отрицательно, то есть 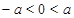 . Отсюда, в силу транзитивности отношения «меньше», следует, что
. Отсюда, в силу транзитивности отношения «меньше», следует, что 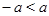 . В этом случае
. В этом случае 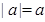 , то есть
, то есть 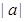 совпадает с большим из двух чисел
совпадает с большим из двух чисел 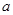 и
и 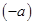 .
.
Если число 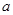 отрицательно, тогда число
отрицательно, тогда число 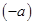 положительно и
положительно и 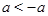 , то есть большим числом является
, то есть большим числом является 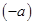 . По определению, в этом случае,
. По определению, в этом случае, 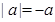 − снова, равно большему из двух чисел
− снова, равно большему из двух чисел 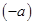 и
и 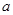 . Теорема доказана.
. Теорема доказана.
Следствие. Для любого действительного числа справедливо: 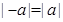 .
.
Доказательство. В самом деле, как 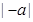 , так и
, так и 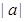 равны большему из чисел
равны большему из чисел 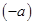 и
и 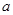 , а следовательно,, равны между собой.
, а следовательно,, равны между собой.
Следствие. Для любого действительного числа 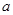 справедливы неравенства
справедливы неравенства 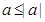 ,
, 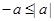 .
.
Доказательство. Умножим второе равенство 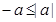 на
на 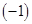 , изменив при этом знак неравенства на противоположный, получим следующие неравенства:
, изменив при этом знак неравенства на противоположный, получим следующие неравенства: 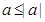 ,
,  справедливые для любого действительного числа
справедливые для любого действительного числа 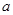 . Объединяя последние два неравенства в одно, получим:
. Объединяя последние два неравенства в одно, получим: 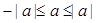 .
.
Модуль числа может быть определен и как наибольшее из чисел a и –a.
Теорема 7. Абсолютная величина любого действительного числа 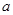 равна арифметическому квадратному корню из
равна арифметическому квадратному корню из 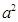 , то есть
, то есть 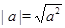 .
.
Доказательство. В самом деле, если 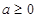 , то, по определению модуля числа, имеем:
, то, по определению модуля числа, имеем: 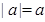 .
.
С другой стороны, при 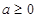 ,
, 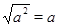 , следовательно,
, следовательно, 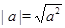 .
.
Если 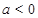 , тогда
, тогда 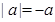 и
и 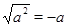 и в этом случае
и в этом случае 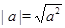 .
.
Теорема доказана.
Теорема 7 дает возможность при решении некоторых задач заменять 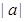 на
на 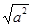 .
.
Для любых действительных чисел справедливы следующие свойства:
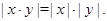
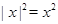 .
.
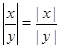 ;
; 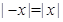 ;
; 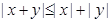 ;
;
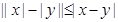 ;
; 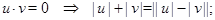
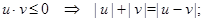
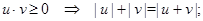
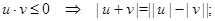
 2015-07-02
2015-07-02 5063
5063
