Варіант 0.
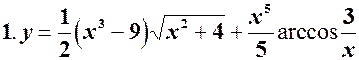
Розв’язання. Похідною алгебраїчної суми функцій є алгебраїчна сума похідних, тобто:
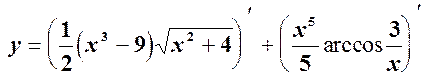
Використовуючи правило диференціювання добутку двох функцій та формули знаходимо:
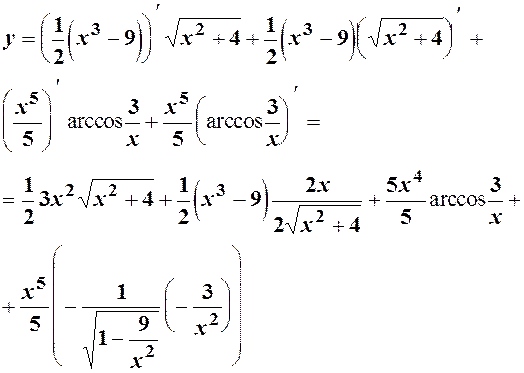
Після скорочення і розкриття дужок остаточно отримуємо:
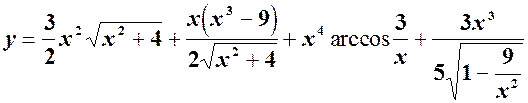
2. 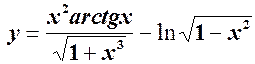
Розв’язання. За правилом диференціювання маємо:
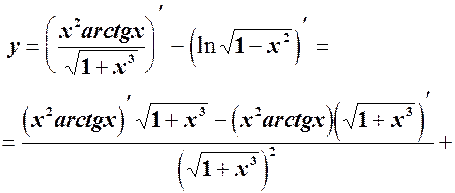
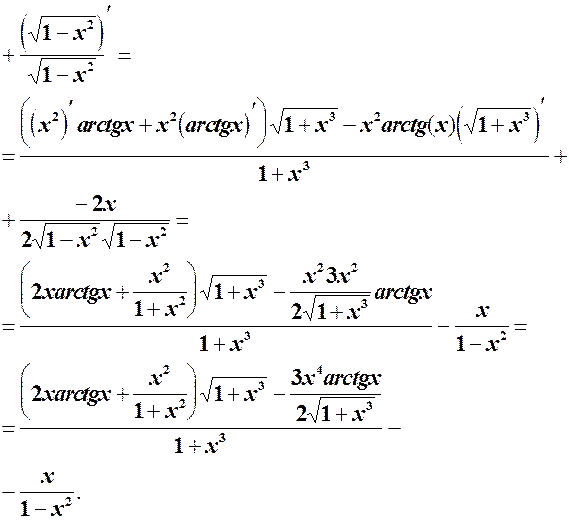
3. 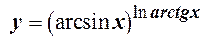
Розв’язання. Для знаходження похідної скористуємось правилом логарифмічного диференціювання.
Спочатку прологарифмуємо функцію за натуральним логарифмом:
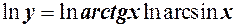
Тому що ln y - складна функція, то
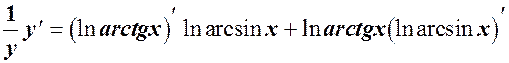
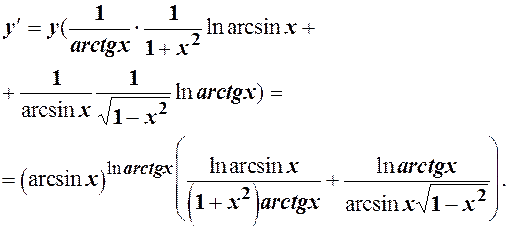
До задачі 4.
Варіант 0:
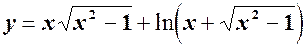
Розв’язання. Використовуючи формулу диференціала функції:
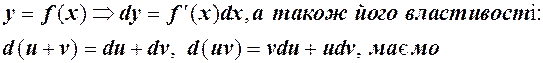
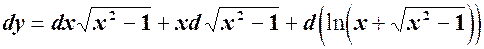
За формулою диференціала
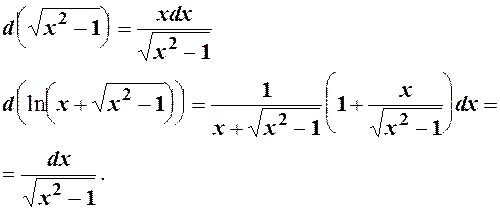
Тоді
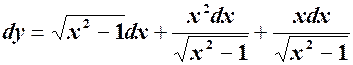
 2015-07-03
2015-07-03 434
434








