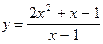Розв’язання

1. Функція визначена та неперервна в інтервалах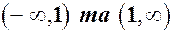

Функція невизначена в точці х = 1.

Знайдемо границі:

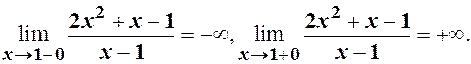
Точки перетину графіка з віссю Х:

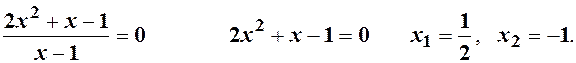
2. Знайдемо асимптоти графіка функції:

а) х=1 - вертикальна асимптота

б)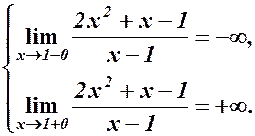

Горизонтальних асимптот немає.

в)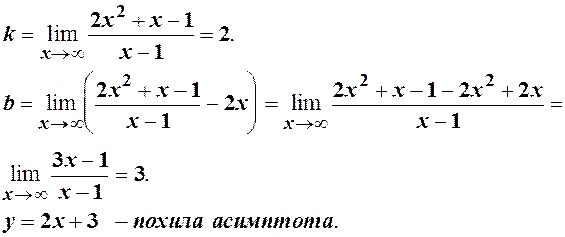

3. Перевіримо функцію на парність:

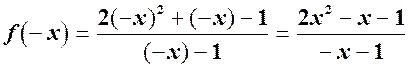
Умови 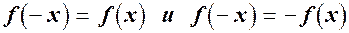не виконуються.

Функція є ні парною, ні непарною.

4. Знайдемо першу похідну.

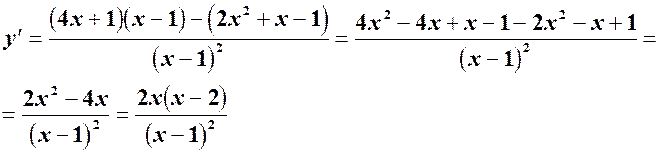Знаходимо точки, в яких похідна дорівнює нулю,

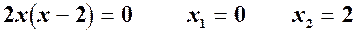. Ці точки розбивають вісь Х на інтервали 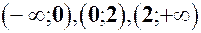. Дослідимо знак похідної на кажному з них:

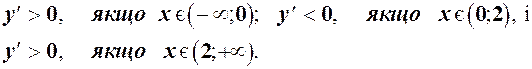
Таким чином, на інтервалах 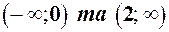функція зростає, а на інтервалі (0,2) функція спадає; точка 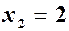- точка мінімума, 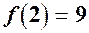; 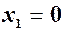- точка максимума, .

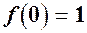5. Знайдемо другу похідну

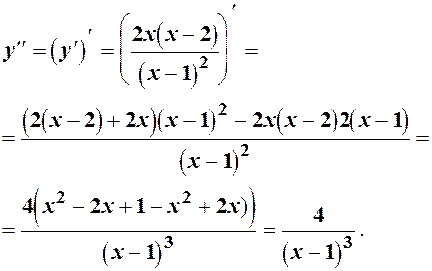
Похідна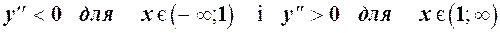

Таким чином графік функції опуклий для при 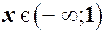і угнутий для .

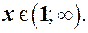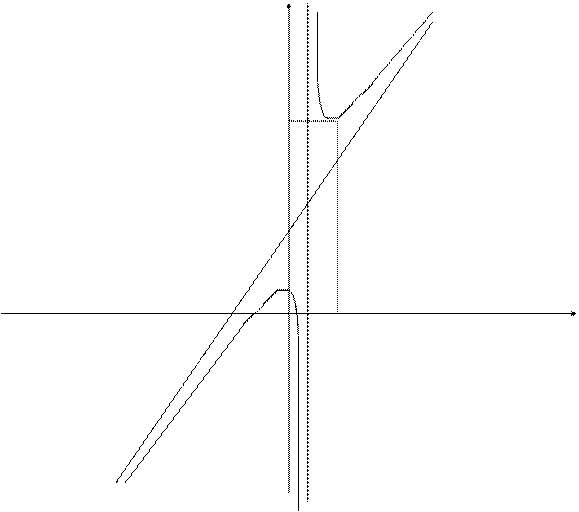
Будуємо на площині X0Y отримані характерні точки: точки перетину з осями 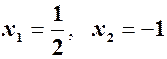, вертикальну асимптоту х=0, похилу асимптоту 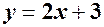, точки екстремума 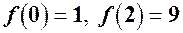. Будуємо графік функції.

Y 9 -1,5 -1 0 1 2 X