Найдем остаток от деления многочлена P (x) на линейный двучлен вида (x ‑ a), где a – некоторое число. Поскольку многочлен‑делитель имеет первую степень, остаток должен иметь нулевую степень, то есть представлять собою некоторое число r. Тогда если Q (x) – многочлен-частное, то имеет место равенство: P (x) = Q (x)·(x ‑ a) + r. Подставив в полученное равенство вместо x число a, получим: P (a) = Q (a)·(a ‑ a) + r = Q (a)·0 + r = r. Таким образом, оказывается, что остаток от деления многочлена P (x) на двучлен (x ‑ a) можно найти, не выполняя деления, подставив в многочлен-делимое a вместо x. Доказанное утверждение, успешно применяемое при решении многих нестандартных задач, составляет суть теоремы Безу (Этье́нн Безу́, 1730 - 1783, французский математик, член Парижской академии наук).
Теорема Безу: Остаток r от деления многочлена P (x) на двучлен (x ‑ a) равен значению этого многочлена в точке a, т.е. r = P (a).
Замечание 1: Многочлен называется приведенным, если его старший коэффициент (т.е. коэффициент при слагаемом наибольшей степени) равен 1. Например, многочлены 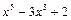 ,
, 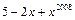 - приведенные, а
- приведенные, а 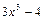 ,
, 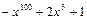 - нет.
- нет.
Замечание 2: При делении многочлена с целыми коэффициентами на приведенный многочлен с целыми коэффициентами все коэффициенты многочлена-частного и многочлена-остатка оказываются также целыми (это легко понять, вспомнив, как выполняется деление многочлена на многочлен «уголком»). В частности, при делении многочлена с целыми коэффициентами на двучлен (x ‑ a), где a – целое число, все коэффициенты многочлена-частного оказываются целыми.
Число a называется корнем многочлена P (x), если P (a) = 0 (другими словами, если число a – корень уравнения P (x) = 0). Например, числа 1 и -1 являются корнями многочлена 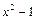 , числа -2 и 5 – корнями многочлена
, числа -2 и 5 – корнями многочлена 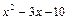 , а многочлен
, а многочлен 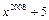 не имеет корней, поскольку невозможно выполнение равенства
не имеет корней, поскольку невозможно выполнение равенства 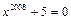 . Из теоремы Безу следует, что если число a является корнем многочлена P (x), то остаток от деления многочлена P (x) на двучлен (x ‑ a) равен P (a) = 0, то есть многочлен P (x) делится на (x ‑ a) без остатка. Другими словами, если a – корень многочлена P (x), то P (x) представим в виде: P (x) = (x ‑ a)· Q (x). Это утверждение составляет суть следствия из теоремы Безу.
. Из теоремы Безу следует, что если число a является корнем многочлена P (x), то остаток от деления многочлена P (x) на двучлен (x ‑ a) равен P (a) = 0, то есть многочлен P (x) делится на (x ‑ a) без остатка. Другими словами, если a – корень многочлена P (x), то P (x) представим в виде: P (x) = (x ‑ a)· Q (x). Это утверждение составляет суть следствия из теоремы Безу.
Следствие из теоремы Безу: Число a является корнем многочлена P (x) тогда и только тогда, когда P (x) делится на (x ‑ a) без остатка.
Задачи:
1. Найдите остаток от деления многочлена 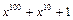 на
на 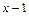 .
.
2. Найдите многочлен третьей степени, который при делении на x дает остаток 1, на x ‑ 2 – остаток 3, а на 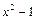 делится без остатка.
делится без остатка.
3. Докажите, что многочлен 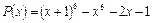 делится на
делится на 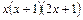 .
.
4. При каких значениях a и b многочлен 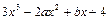 делится без остатка на следующие многочлены:
делится без остатка на следующие многочлены:
а) 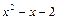 ;
;
б) 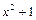 ?
?
5. При делении многочлена на x ‑ 1 в остатке получается 2, а при делении на x ‑ 2 — 1. Каков остаток от деления этого многочлена на 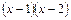 ?
?
6. Найдите остаток от деления многочлена 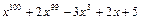 на
на 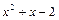 .
.
7. Известно, что остаток от деления многочлена на 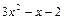 равен 2 x + 1. Найдите остаток от деления этого многочлена на:
равен 2 x + 1. Найдите остаток от деления этого многочлена на:
а) x – 1;
б) 3 x + 2;
в) 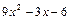 .
.
8. Найдите приведенный многочлен четвертой степени, если известно, что он делится без остатка на 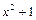 , а при делении на
, а при делении на 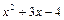 дает в остатке
дает в остатке 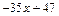 .
.
9. Какими могут быть остатки от деления многочлена P (x) на x – 1, а многочлена Q (x) – на x + 1, если при делении на x 2 – 1 многочлена 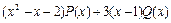 в остатке получается -6?
в остатке получается -6?
10. Докажите, что число 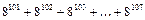 делится на 7.
делится на 7.
11. Докажите, что остатки от деления на 11 чисел 100.000 и 1.000.000.000 равны.
12. Найдите остаток от деления числа 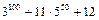 на 26.
на 26.
13. Один из корней уравнения 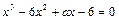 равен 3. Найдите значение параметра a и решите уравнение.
равен 3. Найдите значение параметра a и решите уравнение.
Гал.: стр. 111, №9.10 (б).
Домашнее задание:
14. Не выполняя деления, найдите остаток от деления многочлена 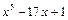 на x + 2.
на x + 2.
15. Какой остаток даёт 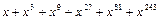 при делении на x ‑ 1?
при делении на x ‑ 1?
16. При каком значении a многочлен 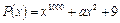 делится на x + 1?
делится на x + 1?
17. Известно, что остаток от деления многочлена на 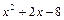 равен 3 x + 2. Найдите остаток от деления этого многочлена на:
равен 3 x + 2. Найдите остаток от деления этого многочлена на:
а) x – 2;
б) x + 4;
в) 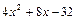 .
.
18. Найдите приведенный многочлен второй степени, который при делении на x – 1 дает в остатке 3, а при делении на x + 2 дает в остатке -4.
19. При каких значениях a и b многочлен 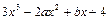 делится без остатка на многочлен
делится без остатка на многочлен 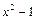 ?
?
20. При каких a и b многочлен 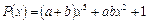 делится на
делится на 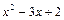 ?
?
21. Многочлен P (x) дает остаток 1 при делении на x – 1 и остаток -1 при делении на x +1. Какой остаток дает P (x) при делении на 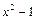 ?
?
22. Найдите остаток от деления многочлена 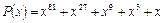
a) на x ‑ 1;
б) на x 2 ‑ 1.
23. Найдите остаток от деления числа 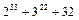 на 7.
на 7.
Гал.: стр. 111, №9.9; №9.10 (а).
А8-1, МАК2008-2009
 2015-07-03
2015-07-03 13812
13812