Многочлены над полем комплексных чисел

К. Гаусс (1777-1855) в нач. XIX в. доказал Основную теорему алгебры.

Всякий многочлен 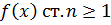над полем комплексных чисел имеет хотя бы один корень, принадлежащий этому полю.

Следствие: Всякий многочлен 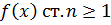над полем комплексных чисел имеет ровно n корней, считая их кратность.

Доказательство:

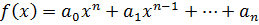
По основной теореме о существовании корня этот многочлен имеет хотя бы 1 корень.

.

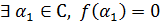Тогда по критерию корня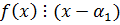

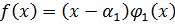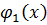, степени .

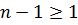По основной теореме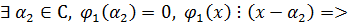

, .

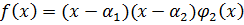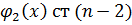Если 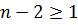, то 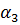корень , .

.

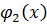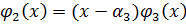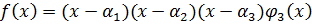На n - ом шаге 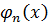- многочлен нулевой степени.

.

.

.

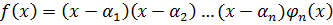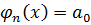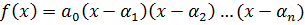Где 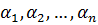- корни.

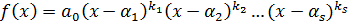, где .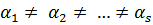

.

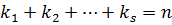2. Всякий многочлен ст. 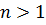является приводимым над полем P.

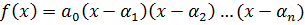- приводим.

Неприводимыми многочленами над полем комплексных чисел являются многочлены 1-ой степени.