Теорема Безу. Следствие из теоремы Безу

Теорема:

Остаток от деления многочлена на линейный двучлен 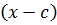равен значению многочлена при .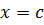

Доказательство:

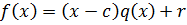
т. к. делиться на 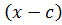, то остаток от деления является числом 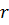не зависящим от x

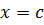
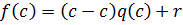
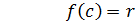
Следствие (критерий того, чтобы многочлен имел корень):

Число является корнем многочлена .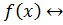

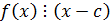Доказательство:

1. Необходимость:

Дано: c – корень .

Доказать: .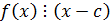

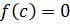(т.к. c – корень).

По теореме Безу .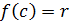

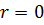
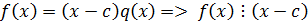
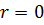
2. Достаточность:

Дано: .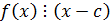

Доказать: c – корень .

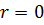(т.к. ).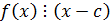

.

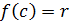
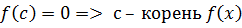Замечание:

По схеме Горнера можно решать следующие задачи:

1) Найти частное и остаток от деления многочлена на линейный двучлен.

2) Находить значение многочлена при любом .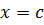

3) Определять является ли число c корнем многочлена.

Нахождение коней многочлена равносильно нахождению его линейных делителей вида .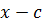

Кратные корни. Теорема о числе корней многочлена 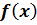n – степени.

Число c называется k – кратным корнем , если 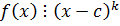, но не делится на .

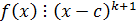Кратность корня многочлена можно определять с помощью схемы Горнера.

Пример: Определить кратность корня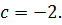

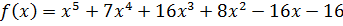
					-16	-16
-2				-4	-8

-2 – корень.

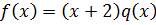
-2

-4

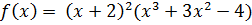
-2

-2

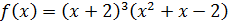
-2

-1

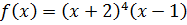
-2

-3

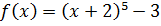
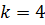
Теорема:

Если имеет степень n, то число корней этого многочлена, принадлежащих полю P, не превосходит n.

Доказательство:

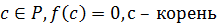
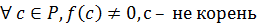
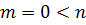
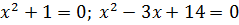
Пусть 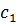– корень .

По следствию из теоремы Безу:

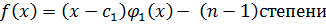
Если 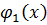не имеет корней над P, то имеет 1 корень.

Пусть 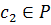- корень .

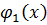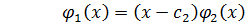
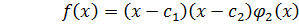
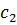– корень , т.к.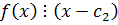

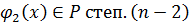
Если 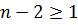продолжим рассуждения.

Пусть 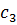– корень .

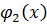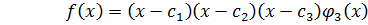
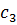– корень .

m – корень.

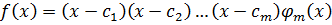
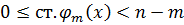
Если бы 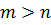, то в правой части ст. больше m, получим противоречие. Следовательно, .

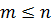Следствие: Нулевой многочлен над любым полем имеет бесконечно много корней.