Основная теорема Алгебры

Дискриминант

Дискриминантом называется многочлен от n переменных 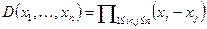. Квадрат дискриминанта является симметрическим многочленом.

Лемма 2.5. Многочлен нечётной степени с вещественными коэффициентами имеет хотя бы один вещественный корень.

Доказательство. Не нарушая общности можно считать старший коэффициент многочлена равным 1. Пусть 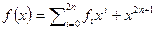, и 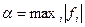. Тогда справедливы неравенства 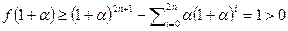и 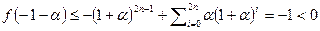. На концах отрезка 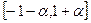многочлен f(x) принимает значения, противоположные по знаку, следовательно, найдётся такое числ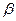о, что .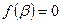

Лемма 2.6. Многочлен второй степени с комплексными коэффициентами имеет комплексные корни.

Доказательство очевидно.

Лемма 2.7 Многочлен с вещественными коэффициентами имеет хотя бы один комплексный корень.

Доказательство. Любое натуральное число, а, значит и степень многочлена n, можно представить в виде произведения , где m – нечётное число. Доказательство проведём методом математической индукции по s. Если s=0, то n – нечётно, и утверждение следует из приведённой выше леммы. Пусть утверждение леммы справедливо для s-1. Покажем его справедливость для s. Рассмотрим многочлен f(x) степени . Построим его поле разложения. В этом поле он имеет корни 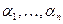. Для некоторого вещественного числа q построим многочлен 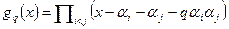. Коэффициенты этого многочлена являются симметрическими многочленами от 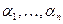, а значит многочленами (с вещественными коэффициентами) от коэффициентов f(x). Степень 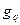равна 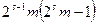, и по предположению индукции многочлен 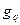имеет комплексный корень. 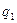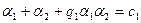Не нарушая общности, можно считать, что найдутся различные вещественные числа и , при которых числа и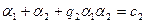- комплексные. Но тогда 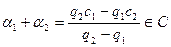и . 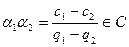Многочлен второй степени 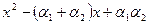имеет комплексные коэффициенты, а значит и его корни 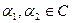. Тем самым лемма доказана.

Теорема 2.19 (Основная теорема алгебры)

Любой многочлен над полем комплексных чисел имеет хотя бы один комплексный корень.

Доказательство. Пусть f(x) многочлен с комплексными коэффициентами 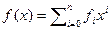. Положим 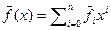и 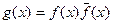. У многочлена g(x) - вещественные коэффициенты, и по доказанному выше, g(x) имеет комплексный корень a, то есть 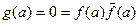. Если f(a)=0, то теорема доказана, a – корень f(x). Пусть 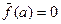. По свойствам операции сопряжения 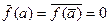, откуда выводим корень f(x).

Следствие 2.8 Многочлен над полем комплексных чисел разлагается в произведение линейных множителей. Разложение единственно с точностью до перестановки сомножителей.

Доказательство. По основной теореме алгебры многочлен f(x) над полем комплексных чисел имеет комплексный корень a, и по теореме Безу, делится на двучлен x-a. Поделим f(x) на x-a и повторим указанные действия с частным. В результате разложим многочлен на линейные множители. Единственность разложения доказана ранее (Теорема 2.8).