Разложение многочленов на неприводимые множители

Основная теорема алгебры.

Любой неконстантный многочлен над полем комплексных чисел имеет хотя бы один корень.

Следствие 1. Любой неконстантный многочлен над полем комплексных чисел разложим в произведение линейных множителей:

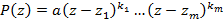
Здесь 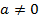 - старший коэффициент многочлена, 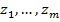– все различные комплексные корни многочлена,  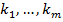- их кратности. Должно выполняться равенство

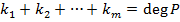
Доказательство этого следствия можно провести индукцией по степени многочлена 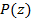. Для линейного многочлена 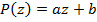утверждение тривиально. Пусть утверждение следствия справедливо для многочленов степени меньше чем 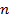и нам дан многочлен степени 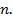Согласно основной теореме алгебры комплексных чисел, многочлен 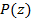имеет корень 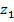. По теореме Безу, разность 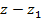делит 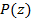, т.е. 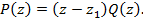Многочлен 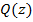имеет степень 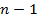и к нему применимо предположение индукции. Разлагая 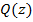а линейные множители, мы тем самым разложим и многочлен 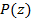на линейные множители. После это следует собрать в одну степень линейные множители с одинаковыми корнями?

Следствие 2. Любой неконстантный многочлен над полем действительных чисел разложим в произведение линейных множителей и квадратных трехчленов с отрицательными дискриминантами:

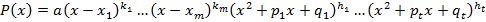
Здесь 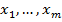 - все различные действительные корни многочлена 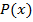, 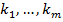-- их кратности, все дискриминанты 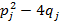меньше нуля, и квадратные трехчлены 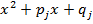все различны.

Доказательство следствия 2 опирается на лемму

Лемма. Пусть 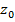 - комплексный корень многочлена 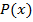с действительными коэффициентами. Тогда сопряженное число 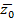есть также корень .

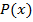Доказательство леммы. Пусть 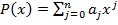. По условию 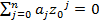. Тогда

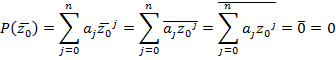
Здесь использовалось равенство 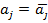и гомоморфность сопряжения.

Доказательство следствия 2 проводим также по индукции как и доказательство следствия 1. База индукции ясна, обоснуем индукционный переход. Пусть 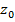 - комплексный корень многочлена 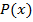. Если 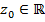, то заканчиваем также как и в доказательстве следствия 1. Пусть 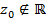, т.е. 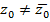. Тогда по теореме Безу, многочлен 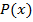представим в виде

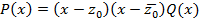
Обозначим 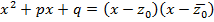, т.е. 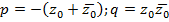. Так как

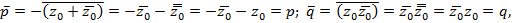
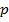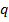то и  - действительные числа. Тогда и  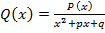- многочлен с действительными коэффициентами, к которому можно применить индукционное предположение.

Доказательство леммы закончено.

Примеры. А. Разложим многочлен 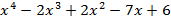на неприводимые множители. Среди делителей константного члена 6 ищем корни многочлена. Убеждаемся, что 1 и 2 – корни. Тем самым многочлен делится на 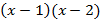. Поделив, находим

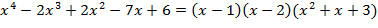
- окончательное разложение над полем 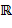, ибо дискриминант квадратного трехчлена 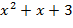отрицателен и, следовательно, он над полем действительных чисел далее не разложим. Разложение того же многочлена над полем комплексных чисел получим, если найдем комплексные корни квадратного трехчлена 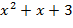. Они суть 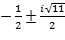. Тогда

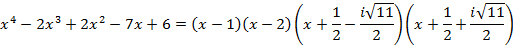
- разложение данного многочлена над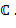

Б. Разложим 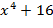над полями действительных и комплексных чисел. Так как действительных корней этот многочлен не имеет, то он разложим на два квадратных трехчлена с отрицательными дискриминантами

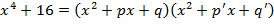
Так как при замене 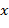на 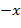многочлен не меняется, то при такой замене квадратный трехчлен 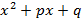должен переходить в 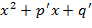и наоборот. Отсюда 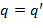и 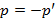. Приравнивая коэффициенты при 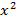получаем 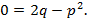В частности, 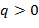. Тогда из соотношения 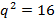(получается подстановкой 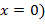извлекаем 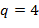, и окончательно, 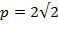. Итак,

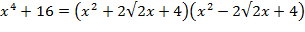
- разложение над полем действительных чисел.

Для того, чтобы разложить данный многочлен над комплексными числами, решим уравнение 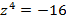по формуле (3) п. 4. Здесь 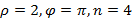. Следовательно,

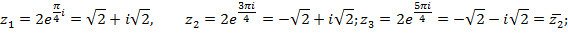
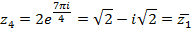
Тогда

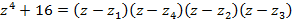
- разложение над комплексными числами. Легко вычислить

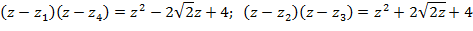
и мы получаем другое решение задачи о разложении многочлена 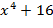над полем действительных чисел.