Наименьшее общее кратное двух и нескольких многочленов

Многочлен 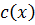называется общим кратным многочленов 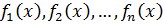, если ,

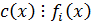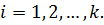
КОН двух или нескольких многочленов называется такой многочлен m(x) над P, который является общим кратным: 1) 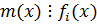; 2) 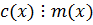; 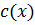- общее кратное.

Теорема:

Для любых двух отличных от нуля многочленов существует НОК.

Теорема:

Если 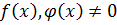, , 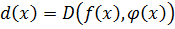то 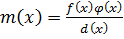является НОК этих многочленов, .

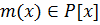Доказательство:

Т.к.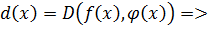

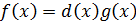
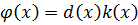
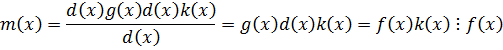
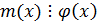
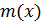- общее кратное.

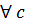общее кратное

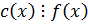
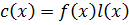
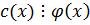
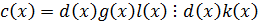
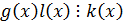
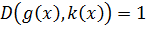
По теореме 2: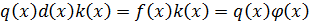

k, q – взаимно простые.

.

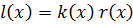
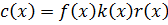
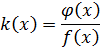
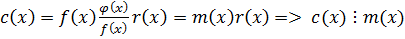Теорема:

Если 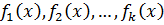– многочлены над полем P и 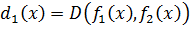, , 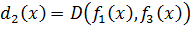…, , 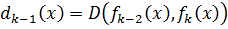то .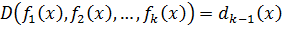

Теорема:

Если 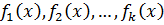– многочлены над полем P и 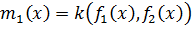, , 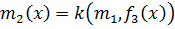, 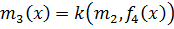…, , 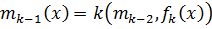то .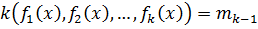

Значение многочлена от числа. Корни многочлена.

Деление многочлена на линейный двучлен.