Иррациональные неравенства
знания и навыки учащихся
Знать определение рационального неравенства, алгоритм решения этого неравенства; уметь решать иррациональные неравенства по алгоритму, а также с помощью графиков.
У р о к
I. Организационный момент.
II. Актуализация опорных знаний.
1. Решить уравнение:
а) 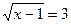 ; б)
; б) 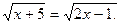
2. Найти ОДЗ неравенства:
а) 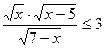 ; б)
; б) 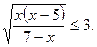
3. Укажите, какой функции:
а) 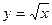 ; б)
; б) 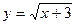 ; в)
; в) 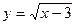 ; г)
; г) 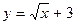
соответствует график:
А. Б. В. Г.
III. Теоретическая часть.
1. Ввести определение иррационального неравенства.
2. 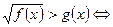
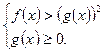
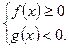
3. 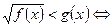
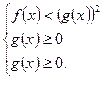
4. Чтобы решить неравенство 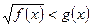 графически, нужно на одном рисунке построить графики функций
графически, нужно на одном рисунке построить графики функций 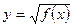 и
и 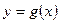 и выяснить при каких значениях х точки графика функции
и выяснить при каких значениях х точки графика функции 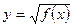 лежат ниже точек графика функции
лежат ниже точек графика функции 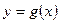 .
.
IV. Практическая часть.
№166(3,5, 6) – на доске по очереди.
Ответ: 3)х 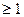 ; 5)х>
; 5)х> 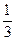 ; 6)0
; 6)0 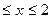 .
.
№167(1) – под диктовку.
№167(3) – за доской.
Ответ: 1)х>11; 3)-22<x 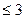 .
.
№170(1, 3) – на доске по желанию
№170(5) – учитель показывает на доске решение.
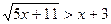
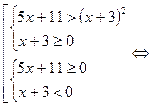
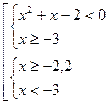

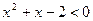
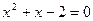
Д=1+8=9
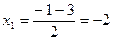 ,
, 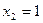
Решение первой системы:
Решение второй системы:
Нет решений.
Ответ: -2<x<1.
№172(1) – учитель показывает на доске решение: 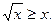
Построим графики функций 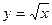 и
и 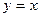 в одной системе координат.
в одной системе координат.
График функции 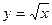 лежит выше графика функции
лежит выше графика функции 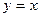 при
при 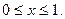
Ответ: 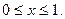
№172(4) – на доске по желанию.
Ответ: 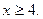
V. Домашнее задание: №166(2, 4); №167(2, 4); №170(4, 6); №172(2, 3).
VI. Итог урока. Объясните алгоритм решения иррационального неравенства.
 2015-07-03
2015-07-03 591
591







