1. Сравните формулы двух функций: 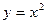 и
и 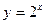 .
.
Первая – степенная, вторая – показательная. Подумайте, почему они так называются. Постройте их графики (показательную по точкам).
Попробуйте построить графики функции 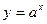 , если
, если 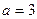 ;
; 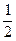 ; 1; -2. Сделайте вывод.
; 1; -2. Сделайте вывод.
2. Функции вида 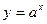 , где а>0, a
, где а>0, a 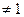 , называется показательной функцией. Она обладает следующими свойствами:
, называется показательной функцией. Она обладает следующими свойствами:
1) Область определения – множество R всех действительных чисел.
2) Область значений – множество всех положительных чисел.
3) Если а>0, то показательная функция возрастает, если 0<a<1, то убывает.
График показательной функции проходит через точку (0; 1) и расположен выше оси 0х.
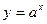
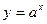
а>1 0<a<1
3. №193 – на доске по желанию.
Ответ: 1)1,7; 2)2,1; 3)0,6; 4)0,2.
№194(3; 4) – за доской.
№195 – устно.
Ответ: 1)1,7 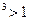 ; 2)0,3
; 2)0,3 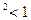 ; 3)3,2
; 3)3,2 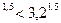 ; 4)
; 4) 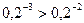 ; 5)
; 5) 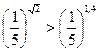 ; 6)3
; 6)3 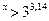 .
.
IV. Домашнее задание: №194(1, 2), №196.
V. Итог урока. Приведите пример показательной функции. Является ли функция 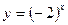 показательной? Почему?
показательной? Почему?
У р о к
 2015-07-03
2015-07-03 527
527








