2015-07-04
647
Метод гармонической линеаризации позволяет представить НЭ линейным динамическим звеном, поведение которого в частотной области эквивалентно поведению НЭ.
Для уяснения сущности гармонической линеаризации рассмотрим НС с одним статическим НЭ (рис. 2.10) и допустим, что на выходе рассматриваемой НС установились гармонические колебания
y (t) = A sinwt. (2.4)
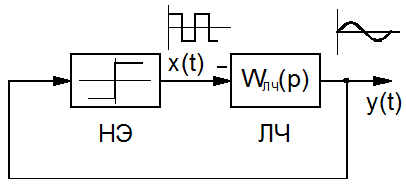
Рис. 2.10. Структурная схема НС с НЭ в управляющем устройстве
Строгости ради отметим, что в реальной системе автоколебания всегда несинусоидальны из-за искажения их формы нелинейным элементом. Однако, если ЛЧ системы включает инерционные звенья, выступающие в роли фильтров низких частот, высшие гармоники автоколебаний не пропускаются системой и можно считать автоколебания синусоидальными. Это допущение называют «гипотезой фильтра».
Чтобы принять его, необходимо проанализировать АЧХ линейной части НС (см., например, рис.2.11). Если в системе установились автоколебания с частотой w 1, то гипотезу фильтра можно принять, так как амплитуда второй гармоники с частотой 2 w 1 очень мала сигналом этой частоты можно пренебречь. Если же частота автоколебаний равна w 2, гипотезу фильтра следует отвергнуть.
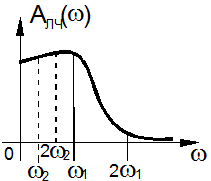
Рис. 2.11. Пример АЧХ линейной части АСУ
Проблема заключается в том, что для выяснения, является ли ЛЧ фильтром нижних частот, следует определить частоту автоколебаний, а сделать это можно только после проведения гармонической линеаризации. Таким образом, применимость метода гармонической линеаризации приходится определять в конце исследования в порядке проверки.
Итак, предположим, что ЛЧ системы является фильтром низких частот и на выходе системы установились гармонические синусоидальные колебания. Эти колебания по каналу обратной связи поступают на вход НЭ. В соответствии с характеристикой НЭ на его выходе устанавливаются колебания несинусоидальной формы (Например, колебания на выходе НЭ, приведенного на рис. 2.10, будут иметь прямоугольную форму (см. рис. 2.12). Периодический сигнал на выходе НЭ можно разложить в ряд Фурье и представить суммой гармоник. Следуя гипотезе фильтра, можем оставить только первую гармонику
x (t) = a 0 + a 1sin wt + b 1cos wt (2.5)
или
x (t) = С 1sin(wt + j) + a 0,
где a 0, a 1и b 1– коэффициенты разложения в ряд Фурье;
С 1 = a 12 + b 12; j = arctg(b 1 / a 1).
Если принять a 0 = 0, то
x (t) = С 1sin(wt + j).
Таким образом, на вход НЭ подали гармонический сигнал и с выхода получили также гармонический сигнал, отличающийся от входного амплитудой и сдвинутый по фазе. Следовательно, в рассмотрение можно ввести некий линейный элемент, эквивалентный рассматриваемому НЭ.
Следует подчеркнуть, что гармоническая линеаризация осуществляется не для отдельного НЭ, а для системы в целом. Поэтому параметры эквивалентного звена зависят не только от характеристики НЭ, но и от параметров ЛЧ системы.
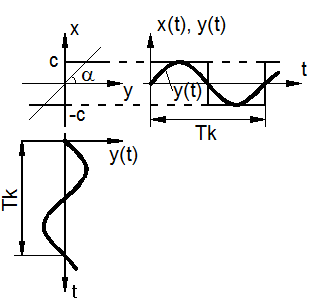
Рис. 2.12. К определению выходного сигнала
релейного двухпозиционного НЭ
На основании (2.4) можем записать
sin wt = y (t) / A и dy/dt = Aw cos wt,
откуда
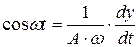. (2.6)
Подставляя выражения для sin wt и cos wt в (2.4), получим
.
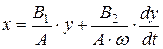Обозначим B 1 / A = q 1; B 2 / A = q 2. Тогда
.
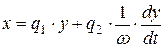Здесь q 1, q 2 – коэффициенты гармонической линеаризации. Их значения зависят от характеристики НЭ и приведены в разд. 5 настоящего пособия (см. табл. В.1).
Представив последнее выражение в операторной форме
,
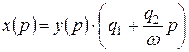можем записать передаточную функцию НЭ
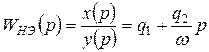. (2.7)
Особенностью передаточной функции НЭ, полученной методом гармонической линеаризации, является наличие частоты, которая никогда не входит в передаточную функцию линейной системы.
Для получения частотной функции необходимо произвести замену p = jw
.
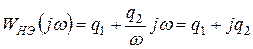Коэффициенты гармонической линеаризации для нелинейности, приведенной нелинейности на рис. 2.10, выражаются как
; 
.
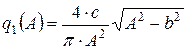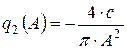Глядя на них, можно сделать вывод, что частотная функция не зависит от частоты, но зависит от амплитуды. Поэтому частотную функцию нелинейного элемента записывают так
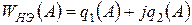. (2.8)
