В релейных системах, как правило, нелинейность сосредоточена в управляющем устройстве. Типичным примером такой системы является релейная следящая система с электрическим исполнительным двигателем. Усиление сигнала рассогласования и управление исполнительным двигателем осуществляется с помощью элементов с релейными характеристиками различного вида.
Использование релейного элемента часто обусловливается необходимостью ограничить амплитуду автоколебаний. Иногда применение релейного элемента позволяет также добиться стабилизации коэффициента усиления системы при изменении коэффициента передачи линейной части, т.е. с введением релейного элемента система приобретает некоторые свойства адаптивных систем.
Рассмотрим возможность создания требуемого автоколебательного режима на примере системы, структурная схема которой приведена на рис. 2.14.
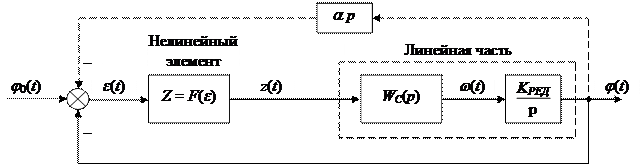 |
Рис. 2.14. Структурная схема релейной следящей системы
На этой схеме WС (р) – передаточная функция замкнутого контура скорости, КРЕД / р – передаточная функция редуктора.
Передаточная функция линейной части
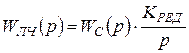 . (2.10)
. (2.10)
Пусть релейный элемент является идеальным реле. Характеристика реле
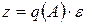 , (2.11)
, (2.11)
где 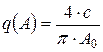 – коэффициент передачи идеального реле по гармонической составляющей (коэффициент гармонической линеаризации). Здесь A 0 – амплитуда на выходе реле при отсутствии задающего воздействия.
– коэффициент передачи идеального реле по гармонической составляющей (коэффициент гармонической линеаризации). Здесь A 0 – амплитуда на выходе реле при отсутствии задающего воздействия.
Таким образом, НЭ может быть заменен эквивалентным коэффициентом усиления q (A), обратно пропорциональным амплитуде входного синусоидального сигнала. Действительно, начиная с некоторого значения амплитуды входного сигнала, НЭ ограничивает амплитуду выходного сигнала. И дальнейший рост амплитуды на входе НЭ уже не приводит к росту амплитуды на его выходе.
Зависимость (2.11) достаточно точно описывает работу реле при отсутствии внешнего сигнала j 0(t) в том случае, если линейная часть является фильтром нижних частот, которые меньше частоты автоколебаний, а более высокие гармоники практически не пропускает. Тогда можно записать
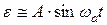 ,
,
где wa – частота автоколебаний.
Передаточная функция НС в замкнутом состоянии
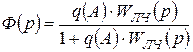 , (2.12)
, (2.12)
где q (A) –
Введем отрицательную обратную связь по производной (пунктир на рис. 2.14). Передаточная функция эквивалентной цепи обратной связи
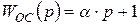 .
.
Пусть
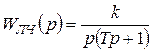 .
.
Уравнение фазовых траекторий
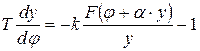 ,
,
где y = dj / dt, а F (e) определяется не только входной величиной j (t), но и ее производной.
На рис. 2.15 приведены фазовые траектории системы (рис. 2.15, а) без дополнительной обратной связи (линия переключения совпадает с осью y) и переходный процесс в системе без дополнительной обратной связи (рис. 2.15, б).
С введением обратной связи по производной уравнение линии переключения примет вид
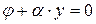 ,
,
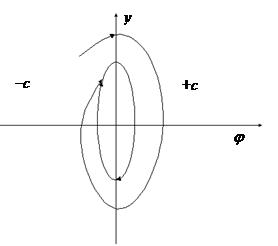
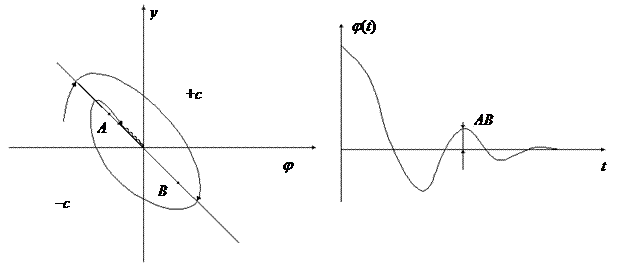
а фазовый портрет преобразуется к виду, показанному на рис. 2.16, а. Переходный процесс в системе с дополнительной обратной связью представлен на рис. 2.16, б.
 | |||
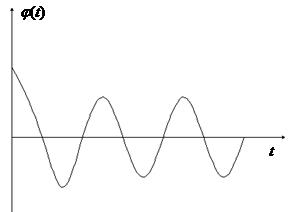 | |||
а) б)
Рис. 2.15. Фазовые траектории (а) и переходный процесс (б) в НС
без дополнительной обратной связи
 |
а) б)
Рис. 2.16. Фазовые траектории (а) и переходный процесс (б) в НС
с дополнительной обратной связью
Введение обратной связи по производной привело к следующему:
- колебательность уменьшилась;
- число колебаний стало конечным;
- на линии пререключения появился участок AB, к которому с двух сторон подходят фазовые траектории, но нет отходящих траекторий.
Изображающая точка, попав на отрезок AB, «скользит» к началу координат.
Следует, однако, отметить, что это кажущееся скольжение. На самом деле точное движение по линии AB невозможно. Дело в том, что любое реле срабатывает не мгновенно, но его переключения происходят с большой частотой и малой амплитудой, что создает эффект скольжения.
Выходная величина изменяется по закону
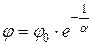 ,
,
т.е. на участке AB процесс становится апериодическим, как в непрерывной системе.
Покажем, как можно определить параметры автоколебаний при введении обратной связи по производной.
Рассмотрим один из методов. Если приравнять нулю характеристический полином замкнутой системы, то получим характеристическое уравнение
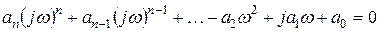 .
.
Для возникновения автоколебаний необходимо наличие в этом уравнении чисто мнимого корня p = jw.
Периодическое решение с найденными параметрами будет существовать, если оно устойчиво. Для исследования устойчивости применим приближенный метод, который заключается в следующем.
Допустим, что вблизи найденного решения (A 0, wa) малым изменениям начальных условий соответствует малое изменение решения, причем вид этого решения сохраняется
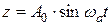 .
.
Таким образом, решение
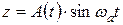 ,
,
где A (t) – медленно меняющаяся со временем амплитуда, которая равна A 0 для периодического решения.
Коэффициент гармонической линеаризации в этом случае можно записать в виде
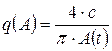 .
.
Можно рассуждать так: если режим автоколебаний устойчив, то при увеличении амплитуды (A > A 0) или при ее уменьшении (A < A 0) возникает переходный процесс, в результате которого восстанавливается режим автоколебаний с прежней амплитудой A 0 (рис. 2.17).
В первом случае амплитуда будет затухать, стремясь к A 0 «сверху», т.е. условие устойчивости для линеаризованной системы выполняется. Во втором случае амплитуда будет возрастать, стремясь к A 0 «снизу», т.е. условие устойчивости для линеаризованной системы не должно выполняться.
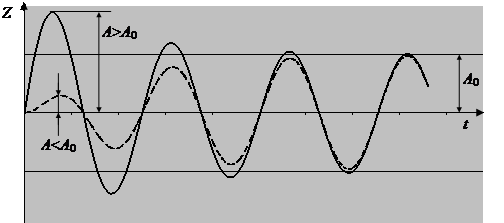 |
Рис. 2.17. Переходные процессы в системе с устойчивыми автоколебаниями
Для оценки устойчивости автоколебаний можно применить критерий Гурвица [2].
 2015-07-04
2015-07-04 2460
2460








