1. Решения 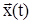 и
и 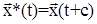 определяют одну и ту же траекторию. Иными словами сдвиг решения по времени не изменяет фазовую траекторию системы (1).
определяют одну и ту же траекторию. Иными словами сдвиг решения по времени не изменяет фазовую траекторию системы (1).
2. Любые две фазовые траектории или не имеют общих точек или совпадают, то есть фазовая траектория не может иметь самопересечений, и две различные фазовые траектории не могут пересекаться.
3. Даже если решение 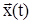 с увеличением t неограниченно приближается к точке покоя
с увеличением t неограниченно приближается к точке покоя 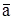 , изображающая точка не может прийти в точку
, изображающая точка не может прийти в точку 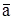 за конечное время.
за конечное время.
4. Если 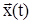 - периодическое решение системы (1), то ему соответствует замкнутая фазовая траектория. (без самопересечений).
- периодическое решение системы (1), то ему соответствует замкнутая фазовая траектория. (без самопересечений).
5. Каждая фазовая траектория является или
а) незамкнутой линией без самопересечений;
b) замкнутой линией без самопересечений;
с) точкой.
Важнейшим вопросом при изучении динамических систем является определение и исследование стационарных (установившихся) движений.
Отметим, что термин движения для обозначения решения системы уравнений (1) заимствован из механики и получил широкое распространение.
а) Наиболее важный тип стационарных движений – это состояния равновесия, которые определяются системой конечных уравнений, получаемых из системы (1), когда производные равны нулю.
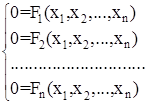 (7)
(7)
Система уравнений (7) имеет некоторое число m решений.
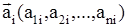 , где i = 1,2…m (8)
, где i = 1,2…m (8)
Следовательно, система (1) имеет решения.
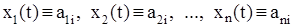 (9)
(9)
Подчеркнем, что соотношение (9) справедливо при изменении t от нуля до бесконечности. Обратим внимание на некоторую терминологическую трудность, решение (9) называются стационарными движениями, хотя им соответствует траектория-точка, которая, естественно, пребывает в неподвижном состоянии.
b) Вторым по важности классом стационарных движений в динамической системе являются периодические движения, то есть такие движения, в процессе которых фазовые переменные совершают колебания с периодом Т:
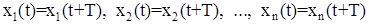 (10)
(10)
Как уже отмечалось траектория, соответствующая периодическим движениям, является замкнутой кривой в фазовом пространстве.
Необходимо различать два принципиально разных вида периодических движений. Это предельные циклы и консервативные движения.
Предельный цикл представляет собой изолированную замкнутую траекторию. В достаточно малой окрестности этой траектории не существует других замкнутых траекторий. Все траектории в этой окрестности или «наматываются» на предельный цикл, либо удаляются от него. (Подробнее этот вопрос будет разъяснен дальше)
Очень важное явление в технике – автоколебания. Автоколебаниям соответствуют в фазовом пространстве устойчивые (понятие устойчивости будет разъяснено дальше) предельные циклы.
Консервативные движения в технических системах встречаются исключительно редко.
c) Третьим видом стационарных движений являются квазипериодические движения. Их еще называют ограниченными непериодическими движениями. Этот вид стационарных движений очень редко встречается в технических системах.
· Перейдем к вопросу об изучении свойств стационарных решений.
Устойчивость положения равновесия.
Введем понятие устойчивость по Ляпунову положения равновесия. Сначала опишем идею, потом приведем формулировку.
Положение равновесия 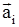 называется устойчивым по Ляпунову, если оно удовлетворяет следующему условию. Пусть начальные условия
называется устойчивым по Ляпунову, если оно удовлетворяет следующему условию. Пусть начальные условия 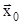 решения
решения 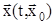 системы (1) достаточно близки к положению равновесия
системы (1) достаточно близки к положению равновесия 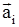 . В этом случае решение
. В этом случае решение 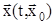 системы будет оставаться близким к точке покоя
системы будет оставаться близким к точке покоя 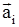 для всех t > 0.
для всех t > 0.
На языке ε-δ это формулируется следующим образом.
Пусть 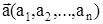 - положение равновесия.
- положение равновесия.
Состояние равновесия 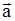 называется устойчивым по Ляпунову, если для каждого заданного (сколь угодно малого) положительного числа ε можно найти такое положительное число δ(ε), что при выполнении неравенств:
называется устойчивым по Ляпунову, если для каждого заданного (сколь угодно малого) положительного числа ε можно найти такое положительное число δ(ε), что при выполнении неравенств:
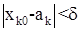 , k = 1, 2, …, n (11)
, k = 1, 2, …, n (11)
для всего бесконечного интервала времени 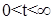 будут справедливы неравенства:
будут справедливы неравенства:
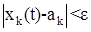 , k = 1, 2, …, n (12)
, k = 1, 2, …, n (12)
Положение равновесия называется асимптотически устойчивым по Ляпунову, если в дополнение к соотношениям (11), (12) имеет место условие:
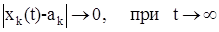 , k = 1, 2, …, n (13)
, k = 1, 2, …, n (13)
Если существует такое ε, что хотя бы в одном случае нельзя найти такое число δ(ε), чтобы при выполнении неравенства (11) выполнялось неравенство (12) для всех t>0, то положение равновесия «а» называется неустойчивым по Ляпунову.
Подчеркнем важное обстоятельство. Из устойчивости одного положения равновесия системы никоим образом не следует устойчивость других положений равновесия. Например, пусть положения равновесия системы (1) будут 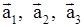 . Возможна ситуация, что
. Возможна ситуация, что 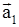 устойчиво, а
устойчиво, а 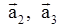 не устойчивы. Или
не устойчивы. Или 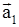 не устойчиво, а
не устойчиво, а 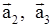 устойчивы.
устойчивы.
Поясним примерами смысл определение устойчивости положения равновесия по Ляпунову.
1. Пусть 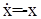
Решение 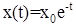
Фазовое пространство одномерно – прямая. Точка равновесия х = 0 асимптотически устойчива, так как при любом значении х0 функция x(t) стремится к нулю при возрастании t.
2. Пусть 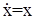
Решение 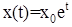 . Точка равновесия неустойчива, так как при любом значении х0 функция удаляется от х = 0.
. Точка равновесия неустойчива, так как при любом значении х0 функция удаляется от х = 0.
3. Пусть 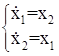
Этой системе соответствует уравнение консервативного звена:
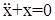
Его решение 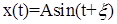 , где А и ξ– постоянные интегрирования. Фазовое пространство двумерно – плоскость.
, где А и ξ– постоянные интегрирования. Фазовое пространство двумерно – плоскость.
Ниже будет показано, что в данной задаче все фазовые траектории представляют собой бесконечное семейство вложенных окружностей с центром в начале координат.
Всегда по заданному ε можно выбрать δ таким образом, чтобы окружность имела радиус меньше ε. Положения равновесия х1 = 0 х2 = 0 устойчиво по Ляпунову, но не асимптотически устойчиво.
· Устойчивость периодических движений.
Определение понятия устойчивости по Ляпунову для периодических движений следующее. Пусть 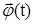 является периодическим решением системы (1). Периодическое решение
является периодическим решением системы (1). Периодическое решение 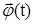 называется устойчивым по Ляпунову, если для каждого заданного положительного числа ε можно найти такое положительное число δ(ε), что из выполнения неравенства
называется устойчивым по Ляпунову, если для каждого заданного положительного числа ε можно найти такое положительное число δ(ε), что из выполнения неравенства
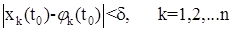 (14)
(14)
Следует, что для любых t>t0 выполняется неравенство
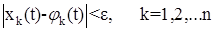 (15)
(15)
Если, кроме того, выполняется условие
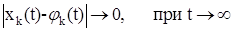 (16)
(16)
То периодическое движение асимптотически устойчиво по Ляпунову.
Понятие устойчивости по Ляпунову положения равновесия исключительно часто используется в науке и технике. С периодическим движением ситуация более сложная. В этом случае ограничения, налагаемые условием устойчивости по Ляпунову, являются слишком жёсткими и выполняются редко. Поэтому для периодических движений используется более слабое условие устойчивости, называемое орбитной устойчивостью.
Периодическое движение 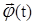 называется орбитно устойчивым, если для любого ε можно найти такое δ(ε), что любая фазовая траектория, которая при t = t0 находится в δ-окрестности траектории периодического движения, для всех t от t0 до бесконечности не выйдет из ε-окрестности траектории периодического движения.
называется орбитно устойчивым, если для любого ε можно найти такое δ(ε), что любая фазовая траектория, которая при t = t0 находится в δ-окрестности траектории периодического движения, для всех t от t0 до бесконечности не выйдет из ε-окрестности траектории периодического движения.
Периодическое движение называется асимптотически орбитно устойчивым, если все упомянутые траектории при t→∞ асимптотически приближаются к траектории периодического движения 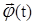 .
.
Поясним понятие окрестности для траектории. Для этого обратимся к рисунку 1, где показана часть замкнутой траектории 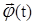 .
.
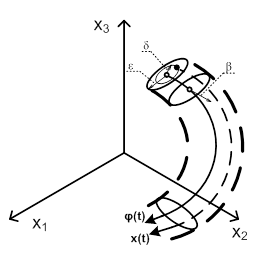
Рис. 1
Под ε- или δ-окрестностью траектории 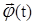 понимается криволинейный цилиндр, который строится следующим образом. Траекторию
понимается криволинейный цилиндр, который строится следующим образом. Траекторию 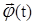 будем рассматривать как тонкую проволоку. Берется круг радиусом ε или δ с дыркой в центре. Этот круг надевается на траекторию, таким образом, чтобы она проходила через центр круга. Затем круг движется по траектории
будем рассматривать как тонкую проволоку. Берется круг радиусом ε или δ с дыркой в центре. Этот круг надевается на траекторию, таким образом, чтобы она проходила через центр круга. Затем круг движется по траектории 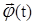 . В процессе его движения плоскость круга должна быть перпендикулярна касательной к траектории
. В процессе его движения плоскость круга должна быть перпендикулярна касательной к траектории 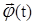 . Поверхность, которая прочерчивает в пространстве окружность данного круга, будет границей криволинейного цилиндра или «бублика». Напоминаем, что траектория
. Поверхность, которая прочерчивает в пространстве окружность данного круга, будет границей криволинейного цилиндра или «бублика». Напоминаем, что траектория 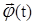 замкнута.
замкнута.
Орбитная устойчивость требует близости не изображающих точек решения 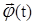 и близкого к нему при t = t0 решения
и близкого к нему при t = t0 решения 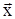 (t), а близости траектории этих точек в пространстве, что, конечно, значительно более слабое условие. Из устойчивости по Ляпунову периодического движения заведомо следует его орбитная устойчивость, но не наоборот. Из орбитной устойчивости не следует устойчивость по Ляпунову периодического движения.
(t), а близости траектории этих точек в пространстве, что, конечно, значительно более слабое условие. Из устойчивости по Ляпунову периодического движения заведомо следует его орбитная устойчивость, но не наоборот. Из орбитной устойчивости не следует устойчивость по Ляпунову периодического движения.
· Методы определения устойчивости положения равновесия.
В 1892 году один из наиболее крупных русских математиков А.М.Ляпунов опубликовал классическую работу «Общая задача об устойчивости движения». В этой работе он предложил два метода исследования устойчивости положения равновесия.
Первый метод: определение устойчивости положения равновесия по уравнению первого приближения. Это уравнение, следуя принятой в технике традиции, будем называть линеаризованным уравнением.
Второй метод (его часто называют прямым методом Ляпунова) сводится к построению некоторых функций, которые называют функциями Ляпунова.
1) Критерий оценки устойчивости в малом положения равновесия по линеаризованной системе (1).
Задачу исследования устойчивости положения равновесия 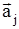 системы (1) можно, используя замену переменных, свести к задаче об устойчивости положения равновесия в начале координат.
системы (1) можно, используя замену переменных, свести к задаче об устойчивости положения равновесия в начале координат.
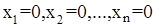 (17)
(17)
Действительно, положим
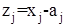 (18)
(18)
Ясно, что
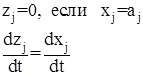 (19)
(19)
Поэтому исходная система
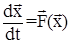 (20)
(20)
преобразуется в систему
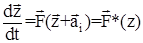 (21)
(21)
Система (20) имеет положение равновесия 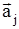 , а система (21) – начало координат.
, а система (21) – начало координат.
Как это принято в литературе, заменим в полученной системе букву z на букву х и опустим звездочку у функции 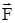 , то есть запишем систему дифференциальных уравнений, формально совпадающую по виду с (20), хотя по существу буквой F у исходной и новой систем обозначены разные функции. (Измененная зависит от
, то есть запишем систему дифференциальных уравнений, формально совпадающую по виду с (20), хотя по существу буквой F у исходной и новой систем обозначены разные функции. (Измененная зависит от 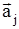 ). Описанное выше переобозначение переменных, если его держать в памяти, не приведет к ошибкам.
). Описанное выше переобозначение переменных, если его держать в памяти, не приведет к ошибкам.
 2015-07-04
2015-07-04 2657
2657
