Замечание

Сформулированные ограничения на функции F_k являются часто слишком жёсткими для систем автоматического управления. Во многих случаях необходимо рассматривать функции F_k, являющиеся кусочно-линейными, разрывными и даже неоднозначными.

Тем не менее, целесообразно начать изучение системы (1) с вышеприведенных, общепринятых в математике классических ограничений для функции F_k, так только в этом случае разработана общая теория.

Рассмотрим некоторые фундаментальные понятия в общем виде, затем перейдем к изучению нелинейных систем второго порядка вида (6)

Отметим, что фактически изучение нелинейных систем мы начнём со случая системы второго порядка:

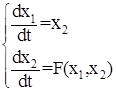(6)

· Фазовое пространство.

Пространство переменных х₁, х₂, …, х_n назовем фазовым пространством, а сами эти переменные – фазовыми переменными или фазовыми координатами.

В теории управления последние годы несколько изменилась терминология, и фазовое пространство называют пространством состояния системы (1) соответственно х₁, х₂, …, х_n – переменными в пространстве состояния. Однако в данной работе мы будем придерживаться «фазовой» терминологии.

Пусть функции х₁(t), х₂(t), …, х_n(t) являются решениями системы (1) при изменении t от 0 до ∞. Для фиксированного момента времени t мы получаем набор чисел, определяющих точку в фазовом пространстве. Если рассматриваем процесс при изменении t, то эту точку будем называть изображающей точкой, а линию, которую она прочерчивает в пространстве при изменении t от 0 до ∞, условимся называть фазовой траекторией.

Иначе можно сказать, что каждое решение системы (1) определяет линию в фазовом пространстве, а если все 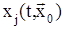постоянные, то оно определяет точку. Эту точку называют «положение равновесия» или «особая точка». Л инию, определяемую решением уравнения (1), называют фазовой траекторией. Это же название используется для случая, когда решением является точка. То есть мы получаем траекторию-точку.