2015-07-04
407
3. В правой полуплоскости нет корней характеристического уравнения, но на мнимой оси есть один или несколько корней (остальные находятся в левой полуплоскости). Этот случай Ляпунов назвал критическим. Для суждения об устойчивости использовать линеаризованную систему (10) нельзя. Необходимо использовать нелинейные члены при разложении функции Fk в ряд.
Необходимо подчеркнуть, что в приведенной теореме под устойчивостью положения равновесия понимается только тот факт, что существует некоторая окрестность ρ, внутри которой решение системы (1) устойчиво, но величина этой окрестности не вычисляется и она может быть весьма малой!
Выше мы обсудили понятие устойчивости положения равновесия в малом, теперь сформулируем еще несколько важных определений понятия устойчивости положения равновесия.
Предположим, что положение равновесия устойчиво в некоторой области G, границы которой нам известны. В этом случае говорят, что положение равновесия устойчиво в большом. Область G может быть невелика, но, разумеется, может быть и очень большой. В соответствии с русским языком, наверное, более уместно было бы говорить об устойчивости в конкретной области, однако, терминология в математике такова, и мы, естественно, будем ей пользоваться.
|
|
|
Пусть система (1) имеет единственное положение равновесия (m = 1) и это положение равновесия устойчиво во всем n-мерном фазовом пространстве.
В этом случае положение равновесия называется устойчивым в целом.
Если единственное положение равновесия асимптотически устойчиво в целом, то говорят, что оно является точкой притяжения для всего фазового пространства.
Подводя итог приведенным определениям устойчивости положения равновесия, обратим внимание, что устойчивость по Ляпунову по смыслу задачи можно назвать – устойчивостью по начальным отклонениям.
2) Применение функции Ляпунова для исследования устойчивости положения равновесия.
Под функцией Ляпунова понимают следующее. Рассмотрим функцию всех фазовых переменных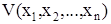 
или сокращенно 
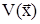. Наряду с функцией V 
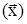введем в рассмотрение функцию 
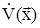, которая является производной функции V в силу системы уравнений (1).
Вычисляем производную функции V:
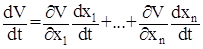(24)
Затем производные функций хi(t) заменяем правыми частями в уравнении (1) – функциями Fi. Получаем:
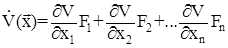(25)
Предположим, что существует область G, внутри которой функция V является дифференцируемой по всем координатам хi.
Теорема Ляпунова утверждает, что нулевое решение устойчиво по Ляпунову, если в области G выполняются следующие условия:
а) V(0) = 0, 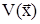>0, если 
;
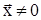b) 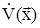≤0
Нулевое решение будет асимптотически устойчиво по Ляпунову, если в условии b) заменить нестрогое равенство на строгое, т.е.
|
|
|
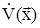<0.
