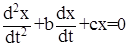 (13)
(13)
Уравнению (13) соответствует система двух уравнений:
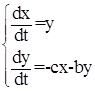 (14)
(14)
Система (14), очевидно, имеет единственную особую точку (точку покоя) – (0,0). Устойчивость этой особой точки целиком определяется корнями характеристического уравнения. От корней характеристического уравнения системы (14) зависит форма фазовых траекторий. Особой точке в зависимости от корней характеристического уравнения присваивается имя собственное:
1. два действительных отрицательных корня – устойчивый узел.
2. два действительных положительных корня – неустойчивый узел.
3. два комплексных корня в левой полуплоскости – устойчивый фокус.
4. два комплексных корня в правой полуплоскости – неустойчивый фокус.
5. два мнимых корня – центр.
6. два действительных корня. Один - положительный, другой – отрицательный – седло.
На фазовой плоскости время может откладываться только параметрическими траекториями.
От системы (14) можно перейти к уравнению фазовых траекторий. Для этого разделим первое уравнение на второе. Получаем:
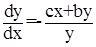 (15)
(15)
Отметим, что из соотношения (15) следует одно важное геометрическое свойство фазовых траекторий: они могут пересекать ось абсцисс только под прямым углом (то есть касательная к траектории должна быть перпендикулярна оси абсцисс). Это следует из того, что при значении у = 0 соотношение (15) обращается в бесконечность. Приведенное геометрическое свойство будет справедливо и для нелинейного уравнения.
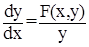
Интегрируя уравнение (15) можно найти выражение для фазовой траектории. Однако, нам удобнее рассмотреть траектории в параметрической форме.
Устойчивый узел.
Решение уравнения имеет вид:
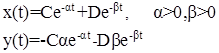 (16)
(16)
Прежде чем рисовать траектории на фазовой плоскости, отметим одно обстоятельство.
Произвольная функция, состоящая из суммы двух экспонент
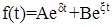 (17)
(17)
не может обратиться в нуль более одного раза (может не обратиться ни разу!).
Действительно
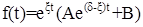 (18)
(18)
Экспонента вообще не может обратиться в нуль, а функция внутри скобок может обратиться в нуль только для одного значения t.
Возвратимся к построению фазовых траекторий для устойчивого узла.
Рассмотрим траектории на фазовой плоскости. Ели одна из постоянных интегрирования обращается в нуль, то соответствующие фазовые траектории расположены на прямых:
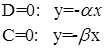 (19)
(19)
(см. рис. 5а)
Следовательно, фазовые траектории, расположены на полупрямых L1 и L*1 и на L2 и L*2.
В общем случае при любых начальных условиях функции х(t) и у(t) стремятся к нулю при t→∞. Изображающая точка может неограниченно приближаться к началу координат только во второй и четвертой четвертях фазовой плоскости.
Для качественного построения фазового портрета мы используем указанные выше факты, условие, что на пути к началу координат фазовая траектория может только один раз пересечь ось ординат (у =0) и ось абсцисс (х = 0), условие, что фазовые траектории не могут пересекаться.
Обратимся к рисунку 5а. Если изображающая точка находится в области Н1 или Н*1 , то она будет двигаться к началу координат только внутри своей области. Та же самая ситуация будет иметь место, если изображающая точка будет находиться в области Н4 и Н*4. Если изображающая точка находится в области Н2 или Н*2, то возможны два варианта в зависимости от начальных условий (ограничимся рассмотрением области Н2):
1) изображающая точка пересекает ось ординат, переходит в область Н3, затем пересекает ось абсцисс и переходит в область Н4, где движется к началу координат;
2) изображающая точка движется к началу координат в исходной области Н2;
В том случае, когда изображающая точка находится в области Н3, то она заведомо пересекает ось абсцисс и движется к началу координат в области Н4.
Аналогичная ситуация имеет место для областей Н*3 и Н*4.
Фазовый портрет для особой точки устойчивый узел показан на рисунке 5b.
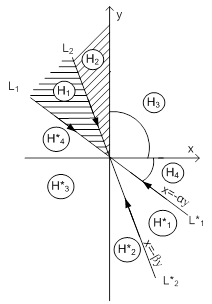 Рис. 5а Рис. 5а |
 2015-07-04
2015-07-04 1644
1644
