Структурное преобразование нелинейных систем. Приведение структурной схемы к канонической форме

Если структурная схема системы имеет один нелинейный элемент, и задача стоит в исследовании собственных движений системы, то ее целесообразно привести посредством структурных преобразований к форме, когда структурная схема будет состоять только из двух блоков – линейного и нелинейного. Такую структурную схему условимся называть канонической. Основная трудность при приведении структурной схемы к канонической форме состоит в том, что нелинейный элемент нельзя менять местами с другими элементами схемы.

Покажем на примерах, как преобразовать к канонической форме структурную схему. Пусть структурная схема имеет вид, показанный на рисунке 1.

Пример 1.

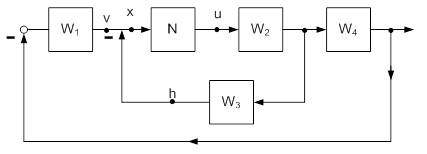
Рис. 1

Запишем уравнение по схеме 1.

h = uW₂W₃ ; v = -uW₂W₄W₁ (1)

x = v – h = -u[W₂W₃ + W₂W₄W₁] = -uW₂[W₃ + W₄W₁] (2)

Уравнениям (1), (2) соответствует схема, показанная на рисунке 2:

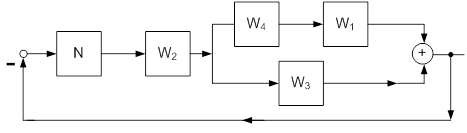
Рис. 2

Схема на рисунке 2 преобразуется к канонической схеме, показанной на рисунке 3.

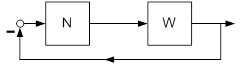
Рис. 3

Где W = W₂[W₃ + W₄W₁]

Пример 2.

Исходная схема имеет вид, показанный на рисунке 4.

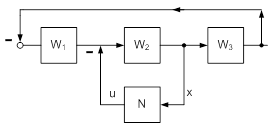
Рис. 4

Запишем уравнение по схеме 4.

[-xW₃W₁ – u]W₂ = x (3)

-uW₂ = [1 + W₃W₁W₂]x (4)

x = -u 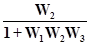(5)

Уравнениям (3), (4), (5) соответствует схема, показанная на рисунке 5:

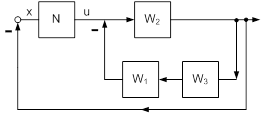
Рис. 5

Схема на рисунке 5 преобразуется к канонической схеме, показанной на рисунке 6.

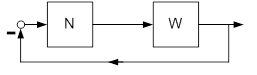
Рис. 6

где W =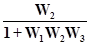

Рассмотрим случай, когда изучаются воздействия на схему внешнего сигнала.

Пусть структурная схема имеет вид, показанный на рисунке 7.

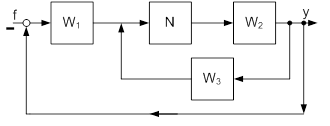
Рис. 7

Делаем очевидные структурные преобразования и получаем схему, показанную на рисунке 8.

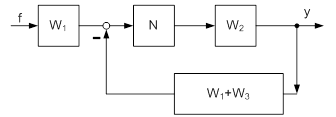
Рис. 8

Схема на рисунке 8 преобразуется к схеме на рисунке 9, где пунктиром выделена каноническая схема.

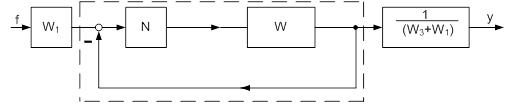
Рис. 9

Где W = W₂(W₃ + W₁)