2015-07-04
330
А)
Рис. 4.
Нелинейность задана в секторе S(μ1,μ2).
|
В)
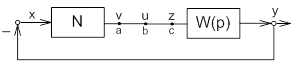Рис. 5.
Фиксируем дополнительные точки съема информации а и с.
Очевидно равенство сигналов v = u = z.
|
С)
Рис. 6.
Охватываем блок W отрицательной обратной связью с коэффициентом λ;
блок N охватываем прямой отрицательной связью с коэффициентом λ.
Непосредственно по схеме записываем соотношение:
x = -y; v + yλ – yλ = z.
Следовательно, v = z. Схемы b и c эквивалентны.
|
D)
Рис. 7.
N0(x) = N(x) – λx; W0(p) =  .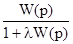
Если положить λ = μ1, то нелинейность в блоке N0,
будет находиться в секторе S(μ0). Где μ0 = μ2 – μ1.
|
Т.к. линейная функция u = μ·x принадлежит классу S[μ1, μ2] или S(μ1, μ2), то первым этапом исследования на абсолютную устойчивость положения равновесия исходной нелинейной системы является рассмотрение вопроса об устойчивости так называемой линейной системы сравнения.
