В силу громоздкости преобразований удобно провести с помощью программы PHASPL пакета TAY3. В теоретическом плане наиболее полное рассмотрение этого вопроса имеется в работе Л.В. Рабиновича.
Ограничимся рассмотрением пример с двухпозиционным реле. Для наглядности используем уравнение в обычной форме. Фактическое изменение касается величины коэффициента усиления.
Передаточная функция объекта:
W(p)= 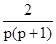
Регулятор: двухпозиционное реле с петлей гистерезиса. a = 0.4: f = 0
Если используется двухпозиционное реле с петлей гистерезиса (положительного), то в системе неизбежны автоколебания, что мы и видим на рисунках 7 и 8.
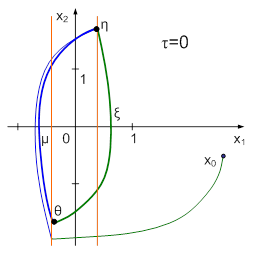 Рис. 5 Рис. 5 | 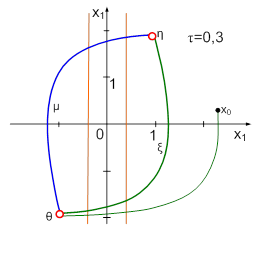 Рис. 6 Рис. 6 |
Двухпозиционное реле с опережением и воздействием по производной f=0.4 (рис.7)
Уменьшение амплитуды автоколебаний
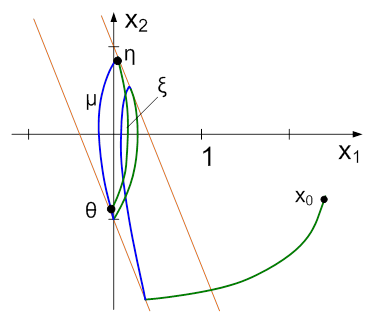 Рис. 7 Рис. 7 |
§6. Точечные преобразования на фазовой плоскости и их применение для расчета релейных систем
Метод точечных преобразований был впервые применен для решения задач теории автоматического управления в 1944 году крупным советским ученым и организатором науки А.А.Андроновым. В последующие десятилетия А.А.Андронову совместно с другими учеными из созданной им Горьковской школы нелинейных колебаний были полностью решены знаменитые задачи авторегулирования, которые сводились к нелинейным дифференциальным уравнениям второго и третьего порядка. Для этих дифференциальных уравнений была исследована зависимость качественных свойств решения (устойчивость положения равновесия, предельные циклы и т.д.) от величины параметров. Были найдены так называемые бифуркационные значения параметров, при которых происходит качественное изменение динамических свойств систем.
В данном параграфе приводятся начальные сведения о методе точечных преобразований и его применении для изучения динамики релейных систем. Изложение базируется на монографии Э.В.Гаушуса, обладающей, на наш взгляд, исключительными методическими достоинствами.
1. Пусть математическая модель изучаемой системы управления может быть записана в следующем виде:

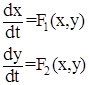 (1)
(1)
Будем рассматривать движение системы (1) на фазовой плоскости. Уравнение фазовых траекторий в данном случае будет иметь вид:
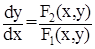 (2)
(2)
Отметим, что в наших задачах y = x’.
Пусть пара функций 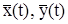 является решением системы (1), для фиксированного значения времени t=t*
является решением системы (1), для фиксированного значения времени t=t* 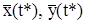 задают координаты изображающей точки. При изменении t от 0 до ∞ функции
задают координаты изображающей точки. При изменении t от 0 до ∞ функции 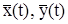 служат параметрическим заданием траектории движения изображающей точки по фазовой плоскости (графика решения уравнения фазовой траектории 2).
служат параметрическим заданием траектории движения изображающей точки по фазовой плоскости (графика решения уравнения фазовой траектории 2).
Предположим, что по мере увеличения t траектория последовательно обходит начало координат. Проведем на фазовой плоскости отрезок Γ, таким образом, чтобы при каждом обходе начала координат траектория пересекала отрезок Γ. Точки пересечения условимся обозначать буквой S.
Фиксируя некоторый момент времени t0,в который траектория (изображающая точка) в очередной раз пересекает отрезок Γ в некоторой точке S, можно построить последовательность возрастающих моментов времени
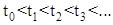 . (3)
. (3)
Последовательности (3) соответствует последовательность точек пересечения отрезка Γ: 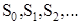
Пусть S –произвольная точка пересечения отрезка Γ в некоторый заданный момент времени. Условимся называть последующей точку S*, соответствующей пересечению отрезка Γ в следующий момент времени, как показано на рисунке 1.
Отметим, что отрезок Γ не обязательно перпендикулярен оси абсцисс, как показано на рисунке 1.
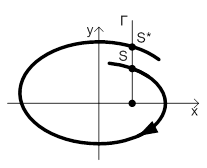
Рис. 1
Введем важное понятие функции последования.
Пусть Ψ – функция, которая для каждой точки пересечения S позволяет вычислить последующую точку пересечения S*:
S* = Ψ(S) (4)
Функция Ψ называется функцией последования для точечного преобразования отрезка Γ в себя.
Зная функцию последования Ψ и приняв за начальную некоторую точку пересечения S0, можно вычислить:
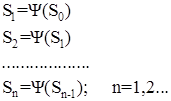 (5)
(5)
То есть с помощью функции последовательно осуществляется итерационный процесс.
Особое значение имеют точки пересечения S, которые преобразуются функцией Ψ в себя:
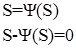 (6)
(6)
Точка отрезка Γ, обозначим ее SN, являющаяся решением уравнения (6), называется неподвижной (или инвариантной) точкой преобразования Ψ.
На фазовой плоскости траектория, являющаяся решением уравнения (2), не может иметь самопересечений, так как она однозначно определяется начальными условиями (в частности координатами точки пересечения отрезка Γ). Поэтому, если траектория походит через неподвижную точку SN, то, значит, изображающая точка движется по замкнутой кривой.
Точечное преобразование отрезка имеет наглядную геометрическую интерпретацию, называемую диаграммой Кенигса-Ламерея.
Пример такой диаграммы показан на рисунке 2.
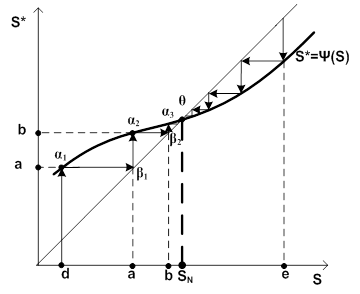
Рис. 2
На рисунке 2 показан первый квадрант действительной плоскости. По оси абсцисс откладывается значения начальных точек, по оси ординат – значения последующих точек. Подчеркнем, что значение начальных и последующих точек на каждом шаге (при каждом обороте изображающей точки на 360º) меняются. Последующая точка становится начальной для некоторой другой последующей точки.
В первом квадранте проведена биссектриса и график функции последования Ψ.
Подробно опишем технику работу с диаграммой. Положим, что начальная точка S0 находится в точке d на оси абсцисс. Проведем из точки d перпендикуляр к оси абсцисс до пересечения в точке α1 с графиком Ψ. Опускаем из точки α1 перпендикуляр на ось ординат. Заключаем, что точка последования S* находится в точке «а». Откладываем значение «а» на оси абсцисс и проводим перпендикуляр до пересечения в точке α2 с графиком Ψ. Из точки α2 опускаем перпендикуляр на ось ординат и определяем, что теперь точка S* находится в точке «b». После этого необходимо отложить значение «b» на оси абсцисс и провести перпендикуляр к оси абсцисс до пересечения с графиком Ψ в точке α3 и т.д.
Указанную последовательность действий проще выполнить иначе. Из точки α1 проводим линию параллельную оси абсцисс до пересечения с биссектрисой в точке β1. Из точки β1 проводим перпендикуляр до пересечения с графиком Ψ. Это пересечение будет иметь место, очевидно, в точке α2. Из точки α2 проводим линию параллельную оси абсцисс до пересечения в точке β2. из точки β2 проводим перпендикуляр, который пересекает график Ψ в точке α3 и т.д.
В результате мы построим «лестницу», по которой будем подниматься (бесконечно) к точке θ, соответствующей неподвижной точке SN.
Если принять, что начальная точка S0 находится в точке «е» оси абсцисс, то аналогично предыдущему мы построим лестницу, по которой будем спускаться (бесконечно) к точке θ.
Из примера на рисунке 2 видно, что неподвижная точка SN может быть пределом последовательности итерационного процесса:
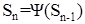 (7)
(7)
Введем понятие устойчивой и неустойчивой неподвижной точки точечного преобразования.
Неподвижная точка SN называется устойчивой, если существует сколь угодно малая окрестность этой точки такая, что любая последовательность (7), начинающаяся в окрестности этой точки сходится к SN. В противном случае неподвижная точка SN называется неустойчивой.
Лестница на диаграмме Кенигса-Ламерея наглядно показывает, устойчива или нет неподвижная точка.
Формальный критерий следующий:
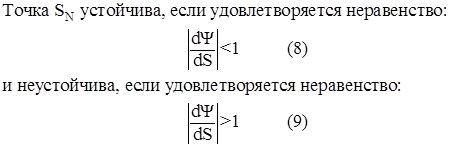
Неравенство для производной приобретает ясный геометрический смысл, если учесть, что биссектриса имеет в любой точке производную, равную единице (в первом квадранте).
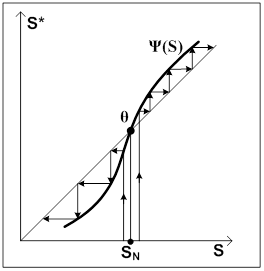
Рис.3
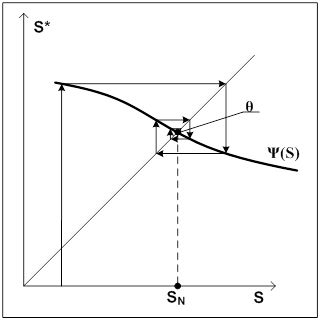
Рис. 4
На рисунке 3 показана неустойчивая предельная точка, а на рисунке 4 – устойчивая.
Функция последования Ψ(S) может иметь конечные разрывы при некоторых значениях переменных. На рисунке 5 показан пример разрывной функции последования.
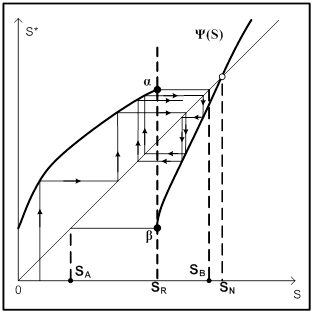
Рис. 5
Функция последования Ψ имеет конечный разрыв, равный отрезку αβ, в точке SR и задается разными аналитическими выражениями при S меньше точки разрыва и при S больше точки разрыва:
Ψ(S)= 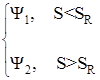 (10)
(10)
Можно показать, и геометрически это наглядно видно, что если 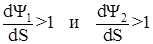 , то точка S не может покинуть отрезка [SA,SB] в процессе вычисления итерации. В этом случае решение дифференциального уравнения совершает ограниченное непериодическое «колебательное» движение, которое называется квазипериодическими колебаниями или движением устойчивым по Пуассону.
, то точка S не может покинуть отрезка [SA,SB] в процессе вычисления итерации. В этом случае решение дифференциального уравнения совершает ограниченное непериодическое «колебательное» движение, которое называется квазипериодическими колебаниями или движением устойчивым по Пуассону.
Рассмотрим случай, когда точечное преобразование задано в параметрической форме:
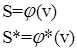 (11)
(11)
В этом случае диаграмма Кенигса-Ламерея строится иначе. Пример такой диаграммы приведен на рисунке 6:
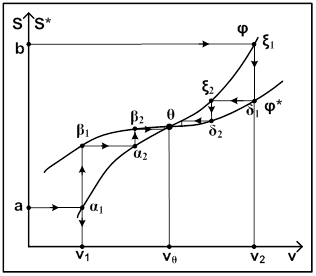
Рис. 6
Опишем работу с диаграммой. Пусть начальное значение S находится в точке «а». Из точки «а» проводим линию параллельную оси абсцисс до пересечения с графиком φ(v) (точка α1). Опуская из точки α1 перпендикуляр на ось абсцисс, определяем значение параметра v, которое соответствует начальной точке, оно равно v1. Продолжая перпендикуляр от точки α1 вверх до пересечения с линией φ*(v) (в точке β1), находим значение последующей точки, соответствующее значению параметра v1. Найденная последующая точка является начальной для следующей итерации. Поэтому из точки β1 проводим параллельно оси абсцисс линию до пересечения с функцией φ и т.д.
Предположим, что значение начальной точки взято в точке «b». Для вычисления значения параметра v, соответствующего взятой начальной точке, проводим линию, параллельную оси абсцисс, до пересечения с функцией φ(v) (в точке ξ1). Затем из ξ1 опускаем перпендикуляр на ось абсцисс и определяем значение параметра, назовем его v2, которое соответствует заданной начальной точке.
Теперь определяем значение последующей точки, соответствующее значению параметра v2. Оно будет определяться с помощью точки δ1. Для его вычисления нужно из точки δ1 опустить перпендикуляр на ось ординат. По оси ординат определяем значение последующей точки.
Теперь последующая точка становится начальной. Проводим из точки ξ2, лежащей на пересечении указанного перпендикуляра с линией φ(v) перпендикуляр к оси абсцисс. Этот перпендикуляр пересечет кривую φ* в точке δ2, из которой проводим перпендикуляр к оси ординат и т.д.
Во избежание неясности, отметим, что на рисунке 6 на графике функции φ(v) находятся точки: α1, α2, θ, ξ1, ξ2. На графике функции φ*(v) находятся точки: β1, β2, θ, δ1, δ2.
Как видно из диаграммы Кенигса-Ламерея на рисунке 6, неподвижная точка (θ) в данном случае устойчива.
В общем случае критерий устойчивости неподвижной точки состоит в том, чтобы при v = vθ выполнялось неравенство:
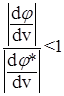 (12)
(12)
Подводя итог, обратим внимание на следующее важное обстоятельство. На сегодняшний день не существует универсального метода вычисления функции последования по заданной системе уравнений (1). В каждом конкретном случае вычисление этой функции является задачей, требующей решения.
2. Перейдем к изучению примеров применения методов точечного преобразования двух релейных систем.
Теперь рассмотрим более подробно с использованием точечного преобразования случай, когда нелинейный элемент является двухпозиционным реле с положительным гистерезисом. Для простоты примем с = а = 1 и f = 1. В этом случае фазовый портрет будет иметь вид, показанный на рисунке 7. В системе возникнут автоколебания, что отразится на фазовой плоскости отразится появлением предельного цикла, областью притяжения которого является вся фазовая плоскость.
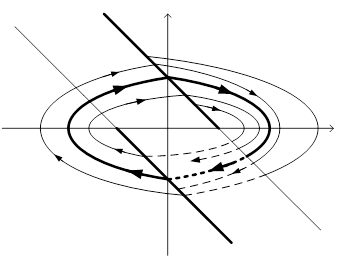 |
Рис. 7
 2015-07-04
2015-07-04 2338
2338








