Основная теорема

1. Пусть W(p) имеет все полюса в левой полуплоскости кроме, быть может, простого полюса в нуле (иначе: пусть W(p) содержит только устойчивые звенья и, быть может, одно интегрирующее звено). В этом случае для абсолютной устойчивости положения равновесия нелинейной системы в классе S(μ₀) достаточно выполнение неравенства В.М.Попова.

2. Если W(p) не содержит интегрирующего звена, а содержит только устойчивые звенья, то выполнение неравенства В.М.Попова достаточно для абсолютной устойчивости положения равновесия в классе S[μ₀].

3. Пусть W(p) содержит устойчивые звенья и два интегрирующих звена. Для того чтобы положение равновесия было абсолютно устойчивым в классе S(μ₀) достаточно выполнение неравенства В.М.Попова и расходимости двух приведённых ниже интегралов

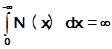
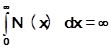(20)

Важно подчеркнуть, что фактически нет необходимости в вычислении интегралов. Их расходимость будет обеспечена, если график N(x) находится на конечном расстоянии от оси абсцисс. В этом случае величина μ₀ не имеет значения, как будет видно из дальнейшего, для выполнения неравенства В.М.Попова.

4. Пусть W(p) наряду с устойчивыми звеньями содержит одно консервативное звено с полюсами ±jΩ и, быть может, одно интегрирующее звено. В этом случае для абсолютной устойчивости положения равновесия в классе S(μ₀) достаточно выполнение неравенства В.М.Попова для всех ω≠Ω. Причём число θ определяется однозначно: 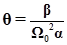(21)

где α и β коэффициенты в разложении W(p) на простые дроби.

В 1961 году была напечатана работа молодого румынского математика В.М.Попова «об абсолютной устойчивости нелинейных систем автоматического регулирования» в журнале «Автоматика и телемеханика» №8. это выдающаяся и исключительно оригинальная работа послужила поворотным пунктом в истории развития теории устойчивости. В дальнейшем значительный вклад в развитие теории абсолютной устойчивости внесли советские математики. Особенно В.А.Якубович.

Условие 3 и 4 данной теоремы были доказаны советским учёным В.Е.Якубовичем (ЛГУ) в 1964 году.