В некоторых случаях задачи оптимального управления можно решать методами вариационного исчисления.
Рассмотрим задачу
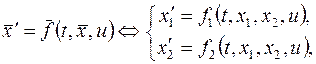 (1)
(1)
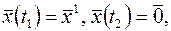 (2)
(2)
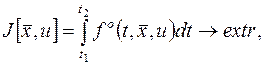 (3)
(3)
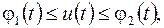 (4)
(4)
где 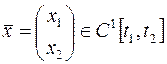 , управление
, управление 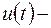 скалярная функция, непрерывная на отрезке
скалярная функция, непрерывная на отрезке 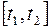 ,
, 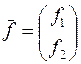 , где функции
, где функции 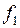 и
и 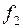 непрерывны как функции четырех переменных
непрерывны как функции четырех переменных 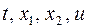 и непрерывно дифференцируемы как функции двух фазовых переменных
и непрерывно дифференцируемы как функции двух фазовых переменных 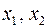 ,
, 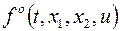 дважды непрерывно дифференцируема как функция четырех переменных
дважды непрерывно дифференцируема как функция четырех переменных 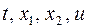 ,
, 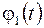 и
и 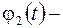 данные скалярные функции, непрерывные на
данные скалярные функции, непрерывные на 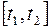 , конец
, конец 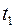 отрезка
отрезка 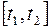 фиксирован, конец
фиксирован, конец 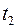 не фиксирован: правые концы графиков функций
не фиксирован: правые концы графиков функций 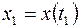 и
и 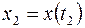 скользят по прямым
скользят по прямым 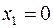 и
и 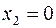 .
.
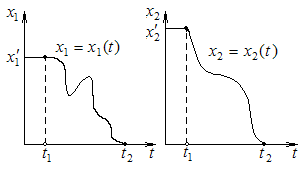
| Без ограничения (4) на управление 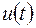 эта задача представляет собой задачу Лагранжа на условный экстремум при уравнениях связи (1). Заметим, что интеграл эта задача представляет собой задачу Лагранжа на условный экстремум при уравнениях связи (1). Заметим, что интеграл 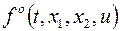 функционала (3) функционала (3)
|
не зависит от производных искомых функций (задача Лагранжа в форме Понтрягина).
Пусть из системы уравнений Эйлера-Пуассона
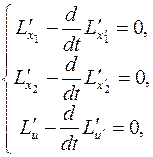 (5)
(5)
где 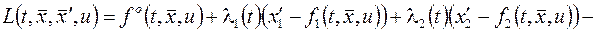 функция Лагранжа,
функция Лагранжа, 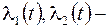 множители Лагранжа, с учетом краевых условий (2) найдены одна или несколько экстремалей
множители Лагранжа, с учетом краевых условий (2) найдены одна или несколько экстремалей 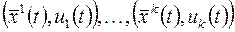 .
.
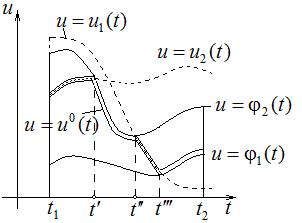
Можно доказать, что если экстремум функционала имеется, то он достигается на функции 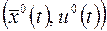 , где управление , где управление 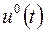 - непрерывная функция, график которой составлен из кусков графиков функций - непрерывная функция, график которой составлен из кусков графиков функций 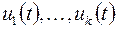 (или некоторых из них), содержащихся (или некоторых из них), содержащихся
| 
|
между графиками 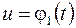 и
и 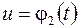 , и кусков графиков функций
, и кусков графиков функций 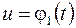 и
и 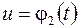 - границ множества допустимых значений управлений. В каких точках
- границ множества допустимых значений управлений. В каких точках 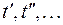 стыкуются куски, можно найти. В этом случае управление
стыкуются куски, можно найти. В этом случае управление 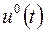 является оптимальным, а функция
является оптимальным, а функция 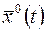 дает соответствующую оптимальную траекторию.
дает соответствующую оптимальную траекторию.
В рассмотренной задаче управление 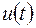 было непрерывным. Однако в большинстве задач оптимального управления оно бывает разрывным (кусочно-непрерывным) и потому применение методов вариационного исчисления затруднено.
было непрерывным. Однако в большинстве задач оптимального управления оно бывает разрывным (кусочно-непрерывным) и потому применение методов вариационного исчисления затруднено.
Возьмем, например, линейную стационарную задачу оптимального быстродействия (п. 2.2):
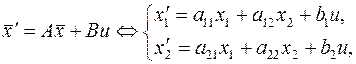
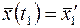 ,
, 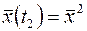 ,
, 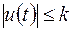 (6)
(6)
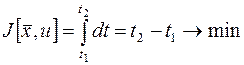
(здесь 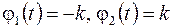 ). Оказывается, что в классе непрерывных управлений
). Оказывается, что в классе непрерывных управлений 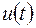 эта задача, вообще говоря, неразрешима.
эта задача, вообще говоря, неразрешима.
Действительно, попытаемся ее решить рассмотренным только что способом. Функция Лагранжа имеет вид (здесь 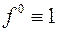 )
)
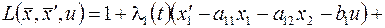
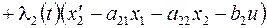 (7)
(7)
Если экстремаль 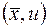 существует, то она удовлетворяет системе уравнений Эйлера-Пуассона (5), которая в нашем случае имеет вид
существует, то она удовлетворяет системе уравнений Эйлера-Пуассона (5), которая в нашем случае имеет вид
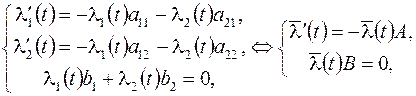
где 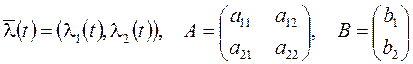 .
.
Продифференцируем по 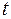 второе равенство:
второе равенство:
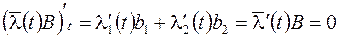 . Исключим
. Исключим 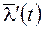 из равенств
из равенств 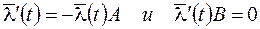 , умножив первое равенство справа на
, умножив первое равенство справа на 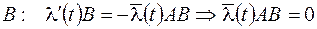 . Получили систему уравнений для
. Получили систему уравнений для 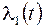 и
и 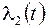 :
:
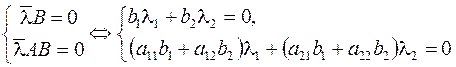 (8)
(8)
с матрицей 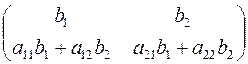 . Ее ранг при транспонировании сохраняется. Транспонированная матрица имеет вид
. Ее ранг при транспонировании сохраняется. Транспонированная матрица имеет вид
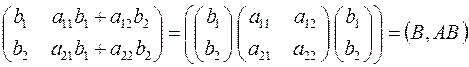 .
.
Согласно критерию Калмана (теорема 2.2.1), система (6) управляема тогда и только тогда, когда 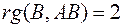 . Следовательно, ранг матрицы системы (8) совпадает с числом неизвестных и потому однородная линейная система (8) имеет единственное (тривиальное) решение
. Следовательно, ранг матрицы системы (8) совпадает с числом неизвестных и потому однородная линейная система (8) имеет единственное (тривиальное) решение 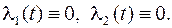 Но тогда функция Лагранжа (7) имеет вид
Но тогда функция Лагранжа (7) имеет вид 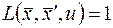 , т.е. не учитывает уравнений связи (6). Однако данная задача без самой системы (6) бессодержательна. Можно доказать, что экстремалей не существует.
, т.е. не учитывает уравнений связи (6). Однако данная задача без самой системы (6) бессодержательна. Можно доказать, что экстремалей не существует.
Если же экстремалей не существует, то оптимальным может быть только управление 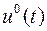 , график которого составлен из кусков графиков функций , график которого составлен из кусков графиков функций 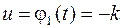 и и 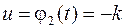 (границ множества допустимых значений управлений). Но остается открытым вопрос, в каких точках (границ множества допустимых значений управлений). Но остается открытым вопрос, в каких точках 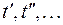
| 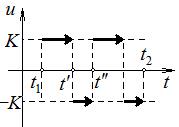
|
происходит переключение управления от значения 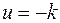 к значению
к значению 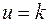 и наоборот. Управление может иметь разрывы.
и наоборот. Управление может иметь разрывы.
Таким образом, рассмотренная задача неразрешима в классе непрерывных управлений.
В 1956г. Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко предложили метод, который обобщил методы классического вариационного исчисления на случай кусочно-непрерывных управлений. В основу этого метода был положен так называемый принцип максимума. В общем случае он сложен. Мы познакомимся с ним в сравнительно простом случае линейной стационарной задачи оптимального быстродействия.
 2015-07-04
2015-07-04 472
472








