Составим сопряженную систему
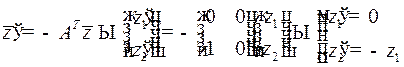 .
.
Ее общее решение 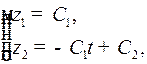 т.е.
т.е. 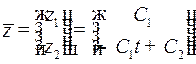 , где
, где 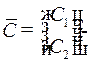 произвольный постоянный вектор.
произвольный постоянный вектор.
Составим функцию Понтрягина:
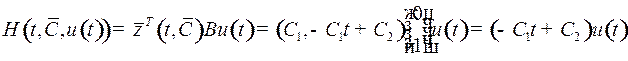 .
.
Пусть 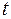 фиксировано. Если
фиксировано. Если 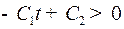 , то среди всех допустимых значений
, то среди всех допустимых значений 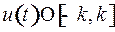 максимальное значение функции Понтрягина доставляет значение
максимальное значение функции Понтрягина доставляет значение 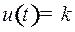 . Если
. Если 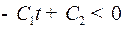 , то функция
, то функция 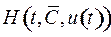 получает максимальное значение при
получает максимальное значение при 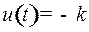 . Таким образом, при всех
. Таким образом, при всех 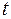 (за исключением значения
(за исключением значения 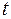 , при котором
, при котором 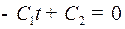 ) функция управления
) функция управления 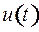 , доставляющая максимум функции Понтрягина, принимает только два значения
, доставляющая максимум функции Понтрягина, принимает только два значения 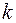 и
и 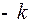 .
.
Отметим, что условие 2 принципа Понтрягина при таком выборе значений 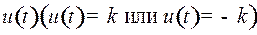 автоматически выполняется:
автоматически выполняется:
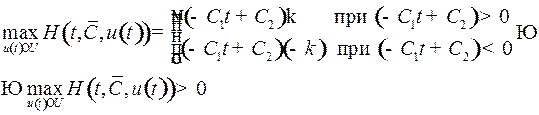
(за исключением одного значения 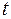 , при котором
, при котором 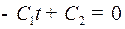 ).
).
Согласно принципу максимума Понтрягина, оптимальные траектории можно получить только при значениях 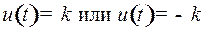 .
.
Пусть 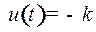 . Тогда система (2) имеет вид
. Тогда система (2) имеет вид 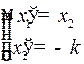 .
.
Ее общее решение
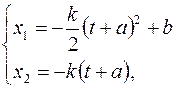 (3)
(3)
где 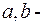 произвольные постоянные (их обозначили
произвольные постоянные (их обозначили 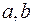 в отличие от постоянных
в отличие от постоянных 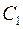 и
и 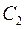 в решении сопряженной системы. Кроме того, вместо
в решении сопряженной системы. Кроме того, вместо 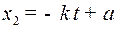 записали
записали 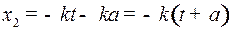 , так как
, так как 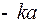 тоже произвольная постоянная, как и
тоже произвольная постоянная, как и 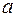 ). Это – семейство оптимальных фазовых траекторий под управлением
). Это – семейство оптимальных фазовых траекторий под управлением 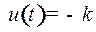 . Исключая время
. Исключая время 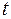 , получим
, получим 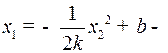 семейство парабол.
семейство парабол.
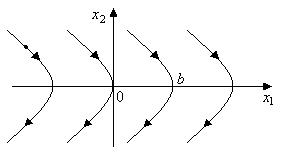
Из уравнения 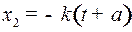 видно, что с увеличением времени видно, что с увеличением времени 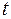 ордината ордината 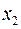 точки точки 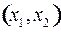 на параболе уменьшается. Следовательно, движение фазовой точки вдоль параболы происходит вниз. на параболе уменьшается. Следовательно, движение фазовой точки вдоль параболы происходит вниз.
| 
|
Пусть 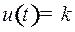 . Тогда система (2) имеет вид
. Тогда система (2) имеет вид 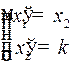 . Её общее решение:
. Её общее решение:
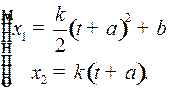 (4)
(4)
Это – семейство оптимальных фазовых траекторий под управлением 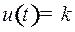 . Исключая
. Исключая 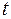 , получаем
, получаем 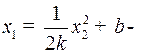 семейство парабол.
семейство парабол.
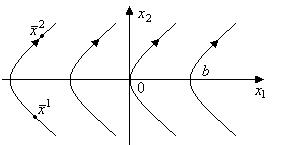
Из уравнения 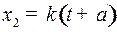 видим, что с возрастанием времени видим, что с возрастанием времени 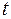 точка точка 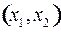 движется вдоль параболы вверх. движется вдоль параболы вверх.
| 
|
Семейства оптимальных траекторий (3) и (4) получены без учета краевых условий. Пока о роли этих семейств можно сказать следующее:
Если точки 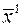 и
и 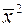 лежат на одной из парабол, то именно кусок этой параболы, соединяющий точки
лежат на одной из парабол, то именно кусок этой параболы, соединяющий точки 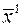 и
и 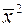 , является оптимальной траекторией (при совпадении направления): объект перейдет из фазового состояния
, является оптимальной траекторией (при совпадении направления): объект перейдет из фазового состояния 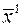 в фазовое состояние
в фазовое состояние 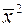 за кратчайшее время именно по этой траектории.
за кратчайшее время именно по этой траектории.
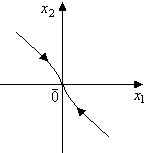
Движение фазовой точки 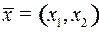 к пункту назначения к пункту назначения 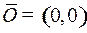 происходит по верхней части параболы семейства (3) при происходит по верхней части параболы семейства (3) при 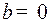 : : 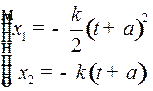
| 
|
по нижней части параболы семейства (4) при 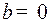 :
:
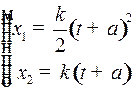 .
.
Линия 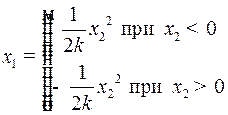 , составленная из кусков парабол семейств (3) и (4), входящих в начало координат, называется линией переключения.
, составленная из кусков парабол семейств (3) и (4), входящих в начало координат, называется линией переключения.
2.5.3. Синтез оптимальной траектории. Пусть точка 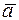 лежит
лежит
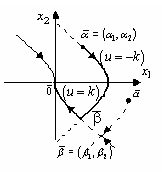
| выше линии переключения. Мы увидим, что оптимальной траекторией окажется траектория, составленная из куска одной из парабол семейств (3) или (4) и куска линии переключения. Двигаясь из точки 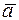 по параболе семейства (4) не попадем ни в начало координат, ни на линию переключения. по параболе семейства (4) не попадем ни в начало координат, ни на линию переключения.
|
Поэтому надо начать движение по параболе семейства (3), которая проходит через точку 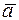 в момент
в момент 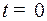 .
.
В некоторый момент 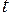 попадем в точку
попадем в точку 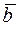 , где эта парабола пересекается с линией переключения. Затем, двигаясь с момента
, где эта парабола пересекается с линией переключения. Затем, двигаясь с момента 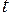 из точки
из точки 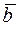 по линии переключения, в момент
по линии переключения, в момент 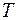 попадем в точку
попадем в точку 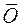 . Полученная траектория и будет оптимальной. В самом деле, проверим выполнение теоремы 2.4.3. При
. Полученная траектория и будет оптимальной. В самом деле, проверим выполнение теоремы 2.4.3. При 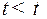 , т.е.
, т.е. 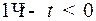 , выбрано управление
, выбрано управление 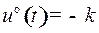 , а при
, а при 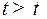 , т.е.
, т.е. 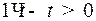 , выбрано управление
, выбрано управление 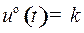 . Значит, на отрезке
. Значит, на отрезке 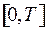 при постоянном векторе
при постоянном векторе 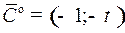 значения
значения 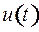 выбраны так, что при каждом фиксированном
выбраны так, что при каждом фиксированном 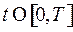 , кроме
, кроме 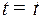 ,
,
1) значение функции Понтрягина
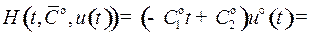
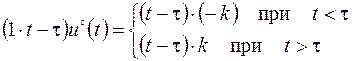 – максимальное среди значений, принимаемых этой функцией при всех
– максимальное среди значений, принимаемых этой функцией при всех 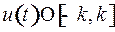 .
.
2) 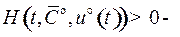 выполняется автоматически, как отмечалось раньше.
выполняется автоматически, как отмечалось раньше.
Условия теоремы 2.4.3 выполнены. Поэтому, согласно принципу максимума Понтрягина, построенная траектория является оптимальной в смысле быстродействия, а соответствующее управление 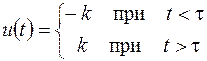 является оптимальным.
является оптимальным.
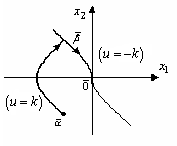
| Аналогично строится оптимальное управление и оптимальная траектория в случае, когда точка 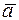 находится ниже линии переключения (в этом случае постоянный вектор находится ниже линии переключения (в этом случае постоянный вектор 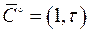 ). Если ). Если 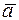 находится на линии переключения, то, очевидно, оптимальной траекторией является кусок самой линии переключения. находится на линии переключения, то, очевидно, оптимальной траекторией является кусок самой линии переключения.
|
 2015-07-04
2015-07-04 679
679








