II. Элементы оптимального управления
Будем рассматривать объект, состояние которого в фиксированный момент времени описывается набором из 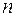 чисел
чисел 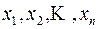 . Например, если объект есть движение материальной точки в пространстве, то
. Например, если объект есть движение материальной точки в пространстве, то 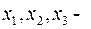 координаты точки; если объект – электрическая цепь, то
координаты точки; если объект – электрическая цепь, то 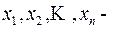 напряжения или токи в различных участках цепи, если объект – течение химической реакции, то
напряжения или токи в различных участках цепи, если объект – течение химической реакции, то 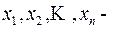 количества различных ингредиентов, катализаторов. Эти числа называют координатами фазового состояния, вектор
количества различных ингредиентов, катализаторов. Эти числа называют координатами фазового состояния, вектор  называется фазовым вектором. Состояние объекта в каждый момент времени можно изобразить точкой (вектором)
называется фазовым вектором. Состояние объекта в каждый момент времени можно изобразить точкой (вектором) 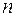 -мерного арифметического пространства
-мерного арифметического пространства 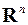 , которое называется фазовым пространством.
, которое называется фазовым пространством.
Движение объекта (например, течение химической реакции) проявляется в том, что его фазовые координаты меняются с течением времени 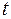 , т.е. фазовый вектор является вектор-функцией
, т.е. фазовый вектор является вектор-функцией 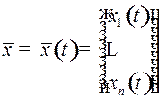 . При движении объекта фазовая (т.е. изображающая) точка
. При движении объекта фазовая (т.е. изображающая) точка 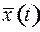 описывает в фазовом пространстве
описывает в фазовом пространстве 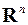 кривую – фазовую траекторию. Обычно фазовые координаты являются инерционными (меняются плавно), так что вектор-функция
кривую – фазовую траекторию. Обычно фазовые координаты являются инерционными (меняются плавно), так что вектор-функция 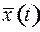 непрерывна.
непрерывна.
Пусть множество 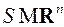 представляет собой совокупность всех фазовых состояний
представляет собой совокупность всех фазовых состояний 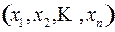 , в которых объекту разрешается находиться. Тогда при движении объекта его состояние
, в которых объекту разрешается находиться. Тогда при движении объекта его состояние 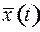 в каждый момент времени
в каждый момент времени 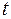 должно подчиняться условию
должно подчиняться условию
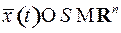 ,
,
которое называется фазовым ограничением.
Предположим, что объект находится под воздействием управления, параметры которого в каждый момент времени описываются набором из 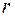 чисел
чисел 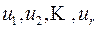 (например, углы поворота рулей, мощность двигателя; в химической реакции – количество добавляемых или убираемых ингредиентов, и т.д.). Этот набор чисел составляет вектор управления
(например, углы поворота рулей, мощность двигателя; в химической реакции – количество добавляемых или убираемых ингредиентов, и т.д.). Этот набор чисел составляет вектор управления 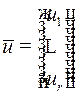 , его можно изобразить точкой (или вектором)
, его можно изобразить точкой (или вектором) 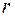 -мерного пространства
-мерного пространства 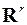 . Управление – вектор-функция
. Управление – вектор-функция 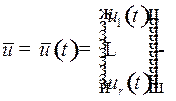 обычно является кусочно-непрерывной функцией (может иметь конечное число скачков в моменты переключения управления). Параметры управления не могут быть совершенно произвольными из-за конструктивных особенностей объекта, ограниченности ресурсов, условий эксплуатации объекта. Это значит, что в пространстве
обычно является кусочно-непрерывной функцией (может иметь конечное число скачков в моменты переключения управления). Параметры управления не могут быть совершенно произвольными из-за конструктивных особенностей объекта, ограниченности ресурсов, условий эксплуатации объекта. Это значит, что в пространстве 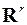 управляющих параметров выделяется некоторое множество
управляющих параметров выделяется некоторое множество 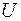 , называемое областью управления. В любой момент времени точки
, называемое областью управления. В любой момент времени точки 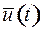 должны принадлежать этому множеству:
должны принадлежать этому множеству:
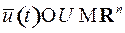 .
.
Это условие называется ограничением на управление. Кусочно-непрерывные функции управления 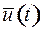 , значения которых попадают в область управления, называется допустимыми управлениями. В дальнейшем имеем в виду допустимые управления. , значения которых попадают в область управления, называется допустимыми управлениями. В дальнейшем имеем в виду допустимые управления. | 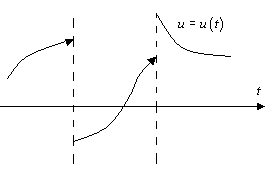 |
Чтобы указать, как именно фазовая траектория объекта 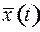 определяется по выбранному управлению
определяется по выбранному управлению 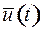 , надо задать закон движения объекта (управляемой системы). Будем предполагать, что закон движения объекта задается системой обыкновенных дифференциальных уравнений
, надо задать закон движения объекта (управляемой системы). Будем предполагать, что закон движения объекта задается системой обыкновенных дифференциальных уравнений
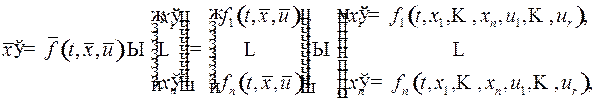 (1)
(1)
где 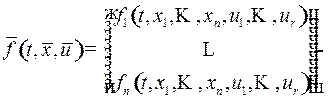 известная вектор – функция, непрерывная как функция
известная вектор – функция, непрерывная как функция 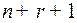 переменных и имеющая непрерывные частные производные по фазовым переменным
переменных и имеющая непрерывные частные производные по фазовым переменным 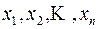 .
.
При фиксированном допустимом управлении 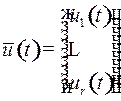 система (1) превращается в нормальную систему обыкновенных дифференциальных уравнений с
система (1) превращается в нормальную систему обыкновенных дифференциальных уравнений с 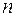 неизвестными функциями
неизвестными функциями 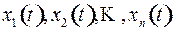 . Её решение
. Её решение 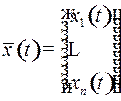 называется фазовой траекторией, соответствующей выбранному управлению
называется фазовой траекторией, соответствующей выбранному управлению 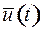 .
.
Говорят, что управление 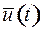 , определенное на отрезке времени
, определенное на отрезке времени 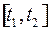 , переводит объект из фазового состояния
, переводит объект из фазового состояния  в фазовое состояние
в фазовое состояние 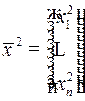 , если соответствующая этому управлению фазовая траектория – решение системы (1) с начальным условием
, если соответствующая этому управлению фазовая траектория – решение системы (1) с начальным условием 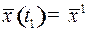 удовлетворяет фазовому ограничению
удовлетворяет фазовому ограничению 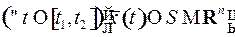 и в момент времени
и в момент времени 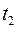 попадает в фазовое состояние
попадает в фазовое состояние 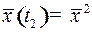 . Таким образом, задача управления состоит в том, чтобы найти какое-нибудь допустимое управление
. Таким образом, задача управления состоит в том, чтобы найти какое-нибудь допустимое управление 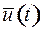 (кусочно-непрерывную функцию из области управления
(кусочно-непрерывную функцию из области управления 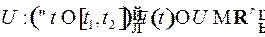 ), чтобы задача (1) с краевыми условиями
), чтобы задача (1) с краевыми условиями 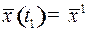 ,
, 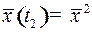 , т.е. задача
, т.е. задача
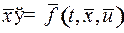 ,
, 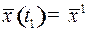 ,
, 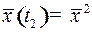 (2)
(2)
имела решение 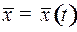 , удовлетворяющее фазовому ограничению
, удовлетворяющее фазовому ограничению
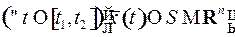 .
.
Если эта задача имеет решение при любых краевых условиях (т.е. всегда найдется допустимое управление 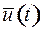 , переводящее объект (1) из любого состояния
, переводящее объект (1) из любого состояния 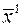 в любое другое состояние
в любое другое состояние 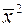 ), то говорят, что система (2) управляема.
), то говорят, что система (2) управляема.
Если система (2) управляема, то обычно она имеет бесконечное множество решений: имеется бесконечно множество допустимых управлений, переводящих объект (1) из фазового состояния 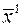 в фазовое состояние
в фазовое состояние 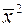 по различным траекториям
по различным траекториям 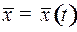 . Поэтому ставится задача оптимального выбора: среди допустимых управлений, решающих задачу (2), выбрать такое, при котором управляемый процесс будет наилучшим в каком-либо смысле. Другими словами, если качество процесса оценивается некоторой числовой характеристикой (себестоимость, время процесса и т.п.), то задача заключается в том, чтобы выбором подходящего управления обеспечить максимальное или минимальное значение этой числовой характеристики. Такую числовую характеристику называют критерием качества. Значение критерия качества определяется фазовой траекторией
. Поэтому ставится задача оптимального выбора: среди допустимых управлений, решающих задачу (2), выбрать такое, при котором управляемый процесс будет наилучшим в каком-либо смысле. Другими словами, если качество процесса оценивается некоторой числовой характеристикой (себестоимость, время процесса и т.п.), то задача заключается в том, чтобы выбором подходящего управления обеспечить максимальное или минимальное значение этой числовой характеристики. Такую числовую характеристику называют критерием качества. Значение критерия качества определяется фазовой траекторией 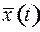 и управлением
и управлением 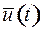 : это – число, зависящее от функций
: это – число, зависящее от функций 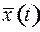 ,
, 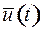 , т.е. функционал
, т.е. функционал 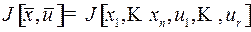 .
.
Задача оптимального управления состоит в отыскании управления 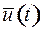 , обеспечивающего экстремум этого функционала:
, обеспечивающего экстремум этого функционала:
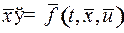 ,
, 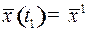 ,
, 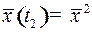 ,
, 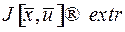 .
.
Управление 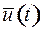 , обеспечивающее экстремум критерия качества
, обеспечивающее экстремум критерия качества 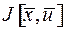 , называется оптимальным управлением, а соответствующая этому уравнению фазовая траектория
, называется оптимальным управлением, а соответствующая этому уравнению фазовая траектория 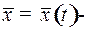 оптимальной траекторией.
оптимальной траекторией.
Наиболее широко используется интегральные критерии качества – функционалы вида
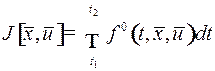 ,
,
где 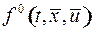 имеет такие же свойства, как и
имеет такие же свойства, как и 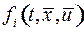 (в смысле непрерывности и дифференцируемости).
(в смысле непрерывности и дифференцируемости).
Мы рассмотрим только одну задачу оптимального управления – линейную стационарную задачу оптимального быстродействия.
 2015-07-04
2015-07-04 954
954







