2015-07-04
276
дифференциальных уравнений. Введем новые неизвестные функци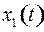и 
и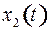 
: 
, 
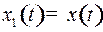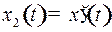. Тогда уравнение движения (1) (уравнение 2-го порядка) сведется к нормальной линейной системе двух дифференциальных уравнений
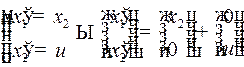с краевыми условиями 
.
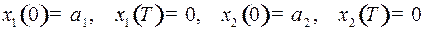Так как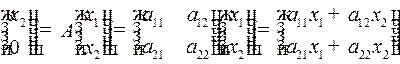 
, то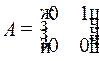 
,
а так как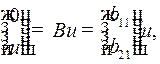 
то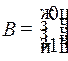 
(
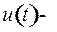скалярная функция: 
).
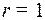Таким образом, имеем стационарную линейную задачу оптимального быстродействия
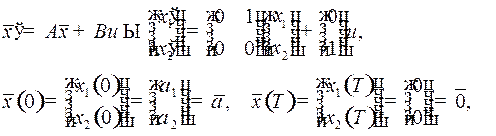
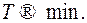(2)
Фазовое ограничение отсутствует: допустимые фазовые состояния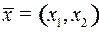 
заполняют всю плоскость: 
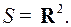На фазовой плоскости первая координата 
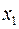точки 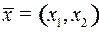означает координату движущейся точки на оси 
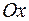, вторая координата 
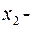скорость точки.
