2015-07-04
349
2.4.1. Определение. Пусть дана однородная линейная система дифференциальных уравнений с постоянными коэффициентами
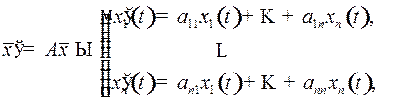
где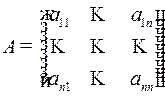 
.
Однородная линейная система дифференциальных уравнений
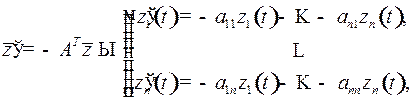(1)
где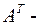 
транспонированная матрица 
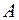, называется сопряженной системо й для данной системы 
.
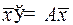Общее решение системы (1) содержит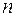 
произвольных постоянных:
,
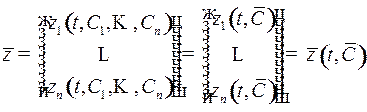т.е. содержат произвольный постоянный n -мерный вектор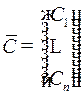 
.
2.4.2. Определение. Функция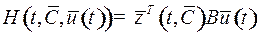 
, где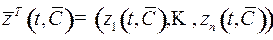 
– общее решение сопряженной системы (1), 
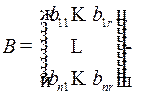матрица управления, 
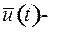управление, называется функцией Понтрягина.
При фиксированном значении момента времени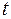 
и постоянного вектора 
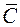значение функции Понтрягина зависит от значения управления 
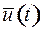в точке 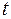: при выборе разных значений управления в фиксированной точке 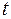функция Понтрягина принимает разные значения.
Формулируем без доказательства принцип максимума Понтрягина:
2.4.3. Теорема (принцип максимума Понтрягина)
Пусть на отрезке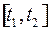 
при некотором постоянном n - мерном векторе 
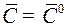допустимые значения управления 
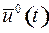(т.е.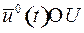 
) выбраны так, что выполняется принцип максимума Понтрягина:
При каждом фиксированном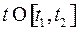 
, за исключением, может быть, конечного числа значений :
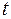1) значение функции Понтрягина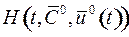 
является максимальным среди значений 
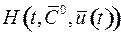, принимаемых при всех других допустимых значениях управления 
:
;
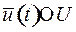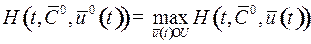2) это максимальное значение положительно: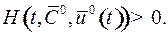 
Тогда управление 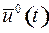на 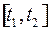является оптимальным по быстродействию.
Далее продемонстрируем применение этого принципа на двух простейших механических задачах.
