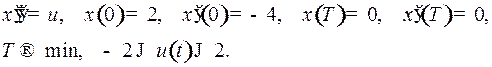
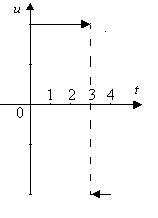
(В момент 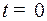 точка проходит через положение
точка проходит через положение 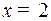 влево со скоростью
влево со скоростью 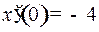 . Нужно остановить ее в положении
. Нужно остановить ее в положении 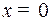 ).
).
□ Пусть 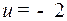 . Решаем систему
. Решаем систему
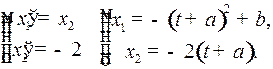 (5)
(5)
Это – семейство парабол 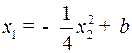 .
.
Пусть  ,
, 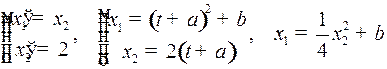 (6)
(6)
Линия переключения
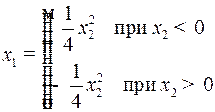 .
Находим закон движения из точки .
Находим закон движения из точки  с момента с момента 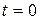 по параболе семейства (6): по параболе семейства (6):
| 
|
полагая 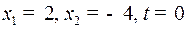 , находим
, находим
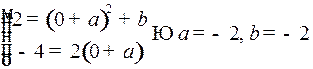 ;
;
Закон движения 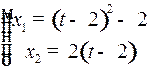 . (7)
. (7)
Это движение происходит по параболе 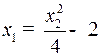 . Найдем точку
. Найдем точку 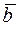 пересечения с линией переключения. Пересечение происходит при
пересечения с линией переключения. Пересечение происходит при 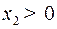 .
.
Поэтому решаем систему уравнений 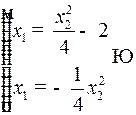
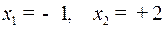 .
.
Находим момент  попадания в эту точку
попадания в эту точку 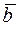 , используя закон движения (7):
, используя закон движения (7): 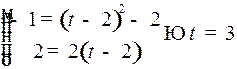 .
.
Находим закон движения из точки 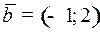 с момента
с момента 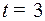 по линии переключения, полагая в (5)
по линии переключения, полагая в (5) 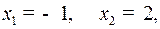 :
: 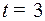 :
:
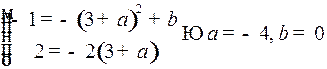 . Закон движения
. Закон движения 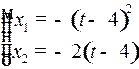 .
.
Наконец, находим момент 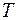 попадания в начало координат
попадания в начало координат 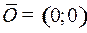 :
:
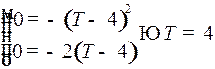 .
.
Итак, оптимальная траектория
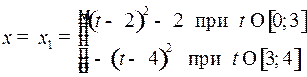 .
Оптимальное уравнение .
Оптимальное уравнение
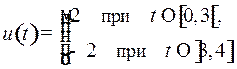 . .
| 
|
Судя по изображенной фазовой траектории, управление движением происходило так:
В момент 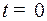 точка проходила положение
точка проходила положение 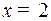 со скоростью
со скоростью 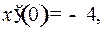 двигаясь влево. Чтобы остановить ее, включили двигатель на полную мощность
двигаясь влево. Чтобы остановить ее, включили двигатель на полную мощность 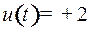 (по оси
(по оси 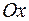 ). Точка остановилась в положении
). Точка остановилась в положении 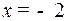 с нулевой скоростью. Под тем же управлением
с нулевой скоростью. Под тем же управлением 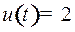 точка двигалась до положения
точка двигалась до положения 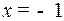 , где имела уже положительную скорость
, где имела уже положительную скорость 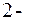 к моменту
к моменту 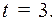 В этот момент, чтобы точка, набирая положительную скорость, не перескочила начало координат, управление переключили на
В этот момент, чтобы точка, набирая положительную скорость, не перескочила начало координат, управление переключили на 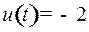 . Это управление затормозило точку и к моменту
. Это управление затормозило точку и к моменту 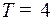 остановило ее в начале координат. ■
остановило ее в начале координат. ■
|
|
|
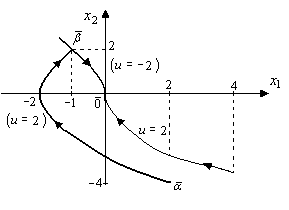
Пример 2. Положим в примере 1 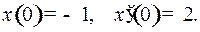
□ Тогда точка 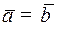 находится на линии переключения. Закон движения из этой
находится на линии переключения. Закон движения из этой
точки с момента 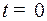
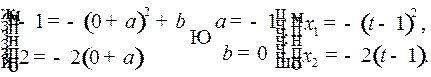
Находим момент 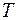 попадания в точку
попадания в точку 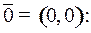
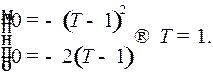 Оптимальная траектория
Оптимальная траектория 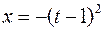 ,
, 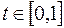 .
.
Оптимальное управление 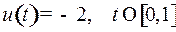 . ■
. ■
 2015-07-04
2015-07-04 314
314








