Математический маятник – груз 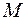 малых размеров с массой
малых размеров с массой 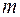 на невесомом стержне
на невесомом стержне 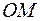 длиной
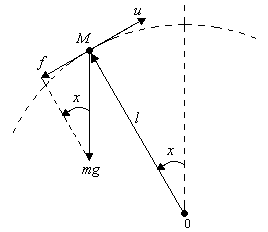
длиной 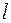 находится вблизи верхнего (неустойчивого) положения равновесия. Требуется под действием ограниченной по величине силы, направленной перпендикулярно к оси маятника, за кратчайшее время привести маятник в положение равновесия с нулевой скоростью (трением пренебрегаем).
находится вблизи верхнего (неустойчивого) положения равновесия. Требуется под действием ограниченной по величине силы, направленной перпендикулярно к оси маятника, за кратчайшее время привести маятник в положение равновесия с нулевой скоростью (трением пренебрегаем).
Обозначим 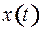 угол отклонения маятника от положения равновесия в момент времени
угол отклонения маятника от положения равновесия в момент времени 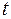 , отсчитываемый в направлении против часовой стрелки.
, отсчитываемый в направлении против часовой стрелки.
 | Управление движением начинается в момент времени 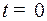 при отклонении при отклонении 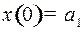 , когда скорость отклонения , когда скорость отклонения 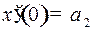 , и должно закончиться за наименьшее время , и должно закончиться за наименьшее время 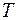 при отклонении при отклонении 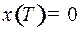 и скорости отклонения и скорости отклонения 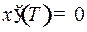 . . |
Управлением является сила 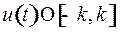
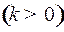 , крайние значения
, крайние значения 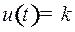 и
и 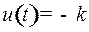 означают включение двигателя на полную мощность в положительном и отрицательном направлении отклонения соответственно.
означают включение двигателя на полную мощность в положительном и отрицательном направлении отклонения соответственно.
Составим уравнение движения маятника. Движение маятника по окружности происходит под действием силы 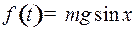 (составляющая силы тяжести в направлении касательной) и управления
(составляющая силы тяжести в направлении касательной) и управления 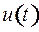 с линейным ускорением
с линейным ускорением 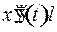 . По второму закону Ньютона
. По второму закону Ньютона
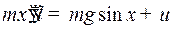 .
.
Это – нелинейное (из-за 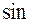 ) дифференциальное уравнение второго порядка с неизвестной функцией
) дифференциальное уравнение второго порядка с неизвестной функцией 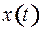 . Ограничиваясь положениями маятника, достаточно близкими к положению равновесия, мы можем заменить
. Ограничиваясь положениями маятника, достаточно близкими к положению равновесия, мы можем заменить 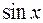 на
на 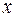 (так как
(так как 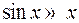 при малых
при малых 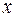 ). Получим линейное дифференциальное уравнение второго порядка
). Получим линейное дифференциальное уравнение второго порядка
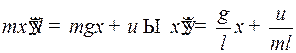 .
.
Для упрощения вычислений будем считать, что 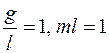 . Тогда имеем уравнение движения
. Тогда имеем уравнение движения
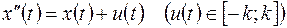 (1)
(1)
с краевыми условиями 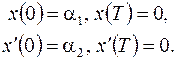
 2015-07-04
2015-07-04 1206
1206
