2015-07-04
487
Если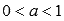 
и а – иррациональное число (например, 
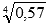), то вид графика степенной функции аналогичен виду графиков, изображенных в этом пункте, свойства степенной функции с иррациональным показателем абсолютно схожи.
Замечание о важности несократимости рациональной дроби в показателе степени.
Не поймите нас неправильно. Здесь мы проводим тонкую грань. Она заключается в том, что графики функци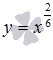й 
и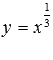 
не совпадают, если не оговорен момент о несократимости показателя степени. Этим мы НЕ ХОТИМ сказать, что 
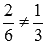, но графики функци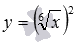й 
и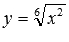 
не соответствуют графику степенной функции .
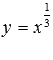Вот тому графическая иллюстрация:
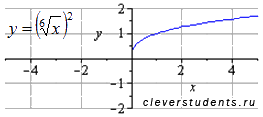
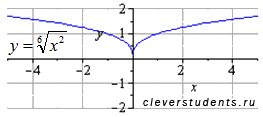
В дальнейшем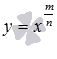 
будем рассматривать как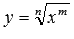 
Рассмотрим степенную функцию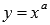 
когда 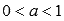, а также числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, причем сама дробь несократима (например, 1/3 или 5/7).
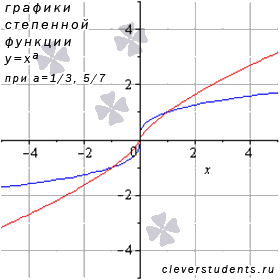
На рисунке представлены графики степенных функций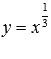 
– синяя линия, 
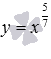– красная линия.
