Свойства степенной функции с отрицательным рациональным показателем

· Область определения: .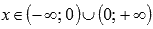
Поведение на границе области определения 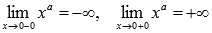при 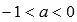и а – несократимая рациональная дробь с нечетным числителем и знаменателем.
Следовательно, х = 0 является вертикальной асимптотой.

· Область значений: .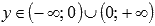

· Функция нечетная, так как .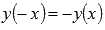

· Функция убывает при .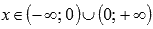

· График функции выпуклый при 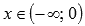и вогнутый при .

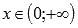· Точек перегиба нет.

· Горизонтальной асимптотой является прямая y = 0.

· Функция проходит через точки (-1;-1), (1;1).

Сейчас поговорим о степенной функции 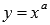, если 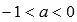и если числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число, а сама дробь несократима (например, -2/3 или -6/7).

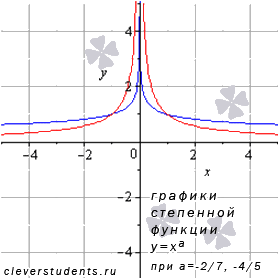
На рисунке показаны графики степенных функций 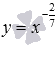– синяя линия, 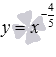– красная линия.