Изображение производных

Чтобы найтн изображение первой производной сигнала, следует выполнить интегрирование по частям:

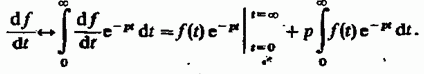
Легко видеть, что изображение первой производной содержит значение сигнала в начальной точке:

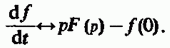
По индукции доказывается формула для изображения производной порядка:

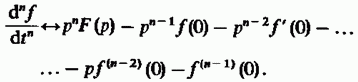
Возможность учитывать начальное состояние сигнала при позволяет применять метод преобразования Лапласа для решения линейных дифференциальных уравнений с известными начальными условиями.

Основные свойства преобразования Лапласа схожи с описанными свойствами преобразования Фурье [14].