В способах вычисления изображений есть много общего с тем, что уже изучалось применительно к преобразованию Фурье. Рассмотрим наиболее характерные случаи.
Пример 2.4, Изображение обобщенного экспоненциального импульса.
Пусть  , где
, где  — фиксированное комплексное число. Наличие
— фиксированное комплексное число. Наличие  -функции обусловливает равенство
-функции обусловливает равенство  при
при  Воспользовавшись формулой (2.54), имеем
Воспользовавшись формулой (2.54), имеем
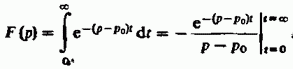
Если  то числитель обратится в нуль при подстановке верхнего предела. В результате получаем соответствие
то числитель обратится в нуль при подстановке верхнего предела. В результате получаем соответствие
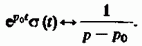
Как частный случай формулы (2.56), можно найти изображение вещественного экспоненциального видеоимпульса:
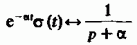
и комплексного экспоненциального сигнала:
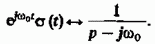
Наконец, положив в (2.57)  , находим изображение функции Хевисайда:
, находим изображение функции Хевисайда:
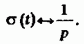
Пример 2.5. Изображение дельта-функции.
Если рассматриваемый импульс возникает в момент времени  , то интеграл
, то интеграл
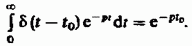
Итак,
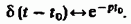
Это изображение определено во всех точках комплексной плоскости  и нигде не имеет особенностей, кроме бесконечно удаленной точки.
и нигде не имеет особенностей, кроме бесконечно удаленной точки.
Некоторую сложность может представлять вычисление изображения дельта-импульса, сосредоточенного при t = 0, поскольку неясно, как надо учитывать вклад от обобщенной функции, сосредоточенной на одном из концов области интегрирования. Дело в том, что в гл. 1 дельта-функция определялась как предел последовательности импульсов, симметричных относительно точки t = 0. Если поступать формально, то в пределах области интегрирования окажется лишь половина такого импульса, что приведет к двукратному уменьшению интеграла. Для того чтобы этого не произошло, изображение функции  определяется как предел
определяется как предел
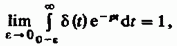
не зависящий от параметра  . При таком подходе функция
. При таком подходе функция  всегда целиком принадлежит области интегрирования, поэтому
всегда целиком принадлежит области интегрирования, поэтому
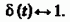
 2015-07-04
2015-07-04 432
432








