Основные соотношения

Пусть — некоторый сигнал, вещественный или комплексный, определенный при t > 0 и равный нулю при отрицательных значениях времени. Преобразование Лапласа этого сигнала есть функция комплексной переменной , задаваемая интегралом:

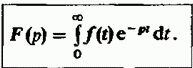
Сигнал называется оригиналом, а функция — его изображением по Лапласу (для краткости, просто изображением).

Условие, которое обеспечивает существование интеграла (2.54), заключается в следующем: сигнал должен иметь не более чем экспоненциальную степень роста при т. е. должен удовлетворять неравенству где — положительные числа.

При выполнении этого неравенства функция существует в том смысле, что интеграл (2.54) абсолютно сходится для всех комплексных чисел , у которых Число а называют абсциссой абсолютной сходимости.

Переменная в основной формуле (2.54) может быть отождествлена с комплексной частотой Действительно, при чисто мнимой комплексной частоте, когда формула (2.54) переходит в формулу (2.16), определяющую Фурье-преобразование сигнала, который равен нулю при Таким образом, преобразование Лапласа можно рассмотри

Подобно тому как это делается в теории преобразования Фурье, можно, зная изображение, восстановить оригинал. Для этого в формуле обратного преобразования Фурье

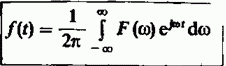
следует выполнить аналитическое продолжение, перейдя от мнимой переменной к комплексному аргументу а На плоскости комплексной частоты интегрирование проводят вдоль неограниченно протяженной вертикальной оси, расположенной правее абсциссы абсолютной сходимости. Поскольку при дифференциал , формула обратного преобразования Лапласа приобретает вид

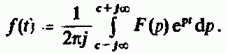
В теории функций комплексного переменного доказано, что изображения по Лапласу обладают «хорошими» свойствами с точки зрения гладкости: такие изображения во всех точках комплексной плоскости , за исключением счетного множества так называемых особых точек, являются аналитическими функциями. Особые точки, как правило, — полюсы, однократные или многократные. Поэтому для вычисления интегралов вида (2.55) можно использовать гибкие методы теории вычетов.