Вопрос 15. Виды случайных сигналов. Примеры, Гауссовский случайный сигнал. Свойства

Различают нестационарные, стационарные и эргодические случайные процессы. Наиболее общий случайный процесс – нестационарный. На рис. 1 приведен пример случайного процесса нестационарного по математическому ожиданию. Случайный процесс X(t) является стационарным, если его многомерная плотность вероятности p(x_1, x₂ , … x_n; t₁,t₂,…t_n) зависит только от величины интервалов t₂-t₁, t₃-t₁,… t_n-t₁, и не зависит от положения этих интервалов в области изменения аргумента t. Отсюда следует, что во-первых, для стационарного процесса одномерная плотность вероятности не зависит от времени т. е.p₁(x,t)=p₁(x); во-вторых, двумерная плотность вероятности зависит от разности t₂-t₁ =t, т.е. p ₂ (x_1, x₂ ; t₁ ,t₂= p₂ (x_1, x₂ ; t) и т. д. В связи с этим все моменты одномерного распределения, в том числе математическое ожидание и дисперсия, постоянны. Часто бывает достаточно для определения случайного процесса стационарным постоянство первых двух моментов. Таким образом для стационарного процесса:

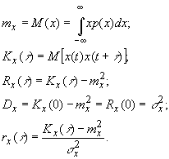
Стационарный случайный процесс называется эргодическим, если при определении любых статистических характеристик усреднение по множеству реализаций эквивалентно усреднению по времени одной бесконечно длинной реализации; в этом случае

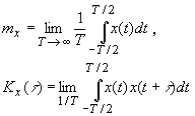
Если x(t) представляет собой случайный ток или напряжение в электрической цепи, то m_x – это постоянная составляющая, а R_x (0)– средняя мощность флуктуаций.

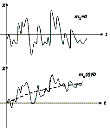
Рис.1

Примеры случайных процессов

1. Гармоническое колебание со случайной амплитудой

Пусть x(t)=Acos(w₀t+q₀)=AcosY(t)

Где w₀и q₀– постоянные величины; А – случайная величина, имеющая равномерную плотность вероятности в интервале от 0 до A _max (рис 4.3 стр.126)

Рис.2

В момент времени t₁ мгновенное значение сигнала может быть любым в интервале от 0 до

A _max cos Y(t₁). Поэтому p(x;t₁)=1/ A _max cos Y(t₁), 0<x< A _max cos Y(t₁)

График имеет вид рис.4.4.

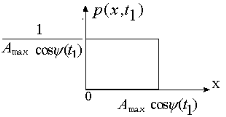
Рис.3

Математическое ожидание такого процесса равно:

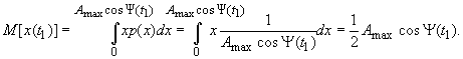
Соответствующие вычисления интегралов дают

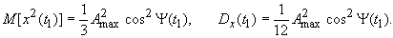
Как видно из приведенных соотношений, первые два момента случайного процесса зависят от времени, а, следовательно, этот процесс нестационарный, и неэргодический.

2. Гармоническое колебание со случайной фазой имеет вид:

x(t)= cos(w₀t+j)

где j- случайная величина, равновероятная в пределах ±π, а плотность вероятности такого случайного процесса равна

p_j(j)=1/2 π, w₀t-π <Y<π

Одна из реализаций имеет вид

x_k(t)= cos(w₀t+q_k)=cosY_k(t)

где Y_k(t)– полная фаза, Y_k(t)– также случайная величина, плотность вероятности которой имеет тот же вид P_Y(Y)=1/2π

Определим вероятность p_x(x)dx того, что в промежутке времени от t₁ до t₁+ dt мгновенное значение сигнала окажется в заданном интервале x, x+dx (рис. 4.5cтр.128):

Рис.4

Эта вероятность совпадает с вероятностью попадания случайной фазы Y в интервалы dYна периоде, которая в свою очередь равна 2p_Y(Y)dY

p_x(x)dx=2p_Y(Y)dY=(2/2π) dY

Таким образом,

p_x(x)=1/π1/ dx/ dY, -1<x<1

Так как

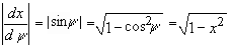
Имеем p_x(x)=(1/π)√1-x², -1<x<1

График этой функции имеет вид, показанный на рис. 5.

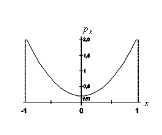
Рис.5

Так как плотность вероятности не зависит от t, то этот процесс является стационарным с математическим ожиданием 1

M_x=1/π ò x/√1-x² dx=0

-1

причем ту же величину можно получить путем усреднения по времени одной реализации:

T/2

x(t)=lim 1/T ò x(t)dt=lim 1/T ò cos(w₀t+q_k)dt=0

T→∞ -T/2 T→∞

что указывает на эргодичность процесса. Корреляционная функция этого процесса равна

R_x(t₁,t₂)=1/2 cos w₀t

3. Нормальный (гауссовский) случайный процесс

Такой случайный процесс характерен для помех канала связи. Одномерная плотность вероятности стационарного эргодического нормального случайного процесса определяется выражением

P(x)=1/√2πσ_x exp[- (x-m_x)²/2σ_x²]

Чем больше σ_x, тем меньше максимум, кривая (рис. 4.7стр.130) более пологая,

Рис.6

причем всегда т. е. площадь под кривой равна 1 для любых. Широкое распространение нормального закона распределения объясняется тем, что при сложении большого числа независимых случайных слагаемых распределение суммы близко к гаусcовскому при любом законе распределения отдельных слагаемых (центральная предельная теорема). Для Гау-

совского случайного процесса с нулевым средним (m_x=0) вероятность того, что модули значений случайной величины превысят величину 3σ_х составляет 0,997≈1, т.е. полный размах такого случайного процесса не превышает 6σ_х (правило трех сигма). Отношение максимумов отклонения случайной величины (пиков) к σ_х называют пик-фактором случайного сигнала. Для гаусовского шума он равен 3, а для гармонического сигнала со случайной фазой √2. Знание p_x(x) не дает полного представления о поведении случайного сигнала во времени. Медленно меняющаяся и быстро меняющиеся случайные функции могут иметь одинаковые плотности вероятности, что отражено на рис. 7.

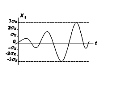
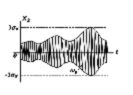
А б

Рис.7

Для оценки этих свойств быстротечности используют корреляционные функции.