нормального распределения при известном 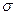
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение 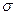 этого распределения известно.
этого распределения известно.
Требуется оценить неизвестное математическое ожидание a по выборочной средней 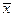 . Поставим своей задачей найти доверительный интервал, покрывающий параметр a
. Поставим своей задачей найти доверительный интервал, покрывающий параметр a
с надежностью 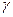 .
.
Будем рассматривать выборочную среднюю 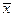 как случайную величину
как случайную величину 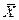 (
(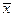 изменяется от выборки к выборке) и выборочные значения признака
изменяется от выборки к выборке) и выборочные значения признака 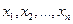 — как одинаково распределенные независимые случайные величины
— как одинаково распределенные независимые случайные величины 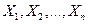 (эти числа также изменяются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение —
(эти числа также изменяются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение — 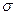 .
.
Примем без доказательства, что если случайная величина X распределена нормально, то выборочная средняя 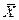 , найденная по независимым наблюдениям, также распределена нормально. Параметры распределения X таковы:
, найденная по независимым наблюдениям, также распределена нормально. Параметры распределения X таковы:
M( 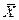 )=a,
)=a, 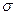 (
( 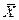 ) =
) = 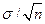
Потребуем, чтобы выполнялось соотношение 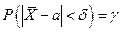 , где
, где 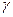 — заданная надежность.
— заданная надежность.
Пользуясь формулой 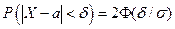 и, заменив X на
и, заменив X на 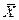 и
и 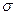 на
на 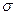 (
( 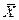 ) =
) = 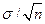 , получим
, получим
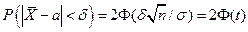 ,
,
где 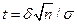 .
.
Найдя из последнего равенства 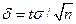 , можем написать
, можем написать
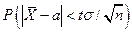 = 2Ф (t).
= 2Ф (t).
Приняв во внимание, что вероятность P задана и равна 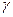 , окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через
, окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через 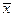 )
)
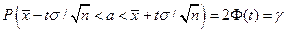 .
.
Смысл полученного соотношения таков: с надежностью 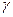 можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал  покрывает неизвестный параметр а; точность оценки
покрывает неизвестный параметр а; точность оценки 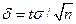 .
.
Число t определяется из равенства 2Ф(t) = 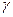 , или Ф(t) =
, или Ф(t) = 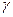 /2; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа Ф(t), равное
/2; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа Ф(t), равное 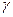 /2.
/2.
Замечание1. Оценку 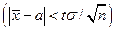 называют классической. Из формулы
называют классической. Из формулы 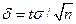 , определяющей точность классической оценки, можно сделать следующие выводы:
, определяющей точность классической оценки, можно сделать следующие выводы:
1) при возрастании объема выборки n число 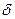 убывает и, следовательно, точность оценки увеличивается;
убывает и, следовательно, точность оценки увеличивается;
2) увеличение надежности оценки 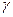 = 2Ф(t) приводит к увеличению t (Ф(t) - возрастающая функция), следовательно, и к возрастанию
= 2Ф(t) приводит к увеличению t (Ф(t) - возрастающая функция), следовательно, и к возрастанию 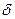 ; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.
; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.
Пример 1. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением 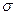 =3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним
=3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним 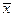 , если объем выборки n=36 и задана надежность оценки
, если объем выборки n=36 и задана надежность оценки 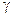 = 0,95.
= 0,95.
Решение. Найдем t. Из соотношения 2Ф(t) = 0,95 получим Ф(t) = 0,475. По таблице находим t = 1,96. Найдем точность оценки: 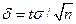 =1,96×3/
=1,96×3/ 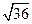 =0,98
=0,98
Доверительный интервал таков: (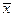 — 0,98;
— 0,98; 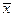 + 0,98).
+ 0,98).
Замечание 2. Если требуется оценить математическое ожидание с наперед заданной точностью 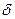 и надежностью
и надежностью 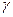 , то минимальный объем выборки, который обеспечит эту точность, то, используя формулу
, то минимальный объем выборки, который обеспечит эту точность, то, используя формулу 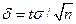 , получаем
, получаем
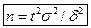 .
.
 2015-07-21
2015-07-21 1451
1451