нормального распределения при неизвестном 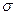
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение 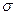 неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором
неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором 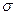 предполагалось известным.
предполагалось известным.
Оказывается, что по данным выборки можно построить случайную величину T (ее возможные значения будем обозначать через t):
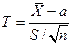 ,
,
которая имеет распределение Стьюдента с k = n - 1 степенями свободы; здесь 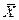 — выборочная средняя, S — «исправленное» среднее квадратическое отклонение, n — объем выборки
— выборочная средняя, S — «исправленное» среднее квадратическое отклонение, n — объем выборки
Число степеней свободы меньше объема выборки на число связей между переменными. Например, если найти среднее значение полученных в результате выборки значений 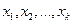 -
- 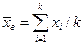 и зафиксировать это значение для соответствующих k случайных величин
и зафиксировать это значение для соответствующих k случайных величин 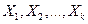 , т. е. признать верным выражение
, т. е. признать верным выражение 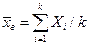 для всех значений этих величин, то одну из величин всегда можно выразить через остальные. Это значит, что она оказалась связанной и система случайных величин потеряла одну степень свободы.
для всех значений этих величин, то одну из величин всегда можно выразить через остальные. Это значит, что она оказалась связанной и система случайных величин потеряла одну степень свободы.
Пользуясь распределением Стьюдента, найдем доверительный интервал
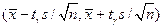 , покрывающий неизвестный параметр а с надежностью
, покрывающий неизвестный параметр а с надежностью 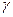 .
.
Здесь случайные величины 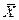 и S заменены неслучайными величинами
и S заменены неслучайными величинами 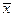 и s, найденными по выборке. По таблице по заданным n и
и s, найденными по выборке. По таблице по заданным n и 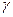 можно найти
можно найти 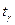 .
. 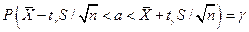
Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n =16 найдены выборочная средняя 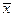 = 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.
= 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.
Решение. Найдем 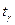 . Пользуясь таблицей, по
. Пользуясь таблицей, по 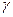 = 0,95 и n = 16 находим
= 0,95 и n = 16 находим 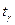 =2,13.
=2,13.
Найдем доверительный интервал: 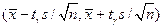
(20,2-2,13  0,8/
0,8/ 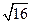 ; 20,2+2,13
; 20,2+2,13  0,8/
0,8/ 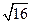 ) ^ (19,774; 20,626)
) ^ (19,774; 20,626)
Распределение 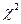
 2015-07-21
2015-07-21 1070
1070








