отклонения 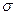 нормального распределения
нормального распределения
Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение 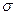 по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр
по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр 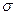 с заданной надежностью
с заданной надежностью 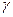 .
.
Потребуем, чтобы выполнялось соотношение
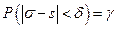 , или
, или 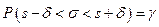 .
.
Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство 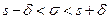 в равносильное неравенство
в равносильное неравенство 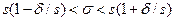 .
.
Положив 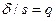 , получим
, получим
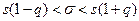 . (
. (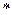 )
)
Остается найти q. С этой целью введем в рассмотрение случайную величину 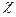 «хи»:
«хи»: 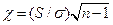 , где n - объем выборки.
, где n - объем выборки.
Величина 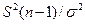 распределена по закону
распределена по закону 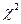 с n - 1 степенями свободы, поэтому квадратный корень из нее обозначают
с n - 1 степенями свободы, поэтому квадратный корень из нее обозначают 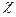 . Плотность распределения
. Плотность распределения 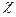 имеет вид
имеет вид
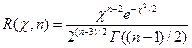
Преобразуем неравенство (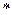 ) так, чтобы оно приняло вид
) так, чтобы оно приняло вид 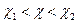 . Вероятность его равна заданной вероятности
. Вероятность его равна заданной вероятности 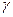 :
:
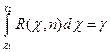
Полагая, что q < 1, перепишем неравенство (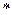 ):
):
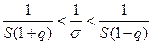
Умножив все члены неравенства на 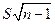 , получим
, получим
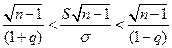
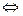
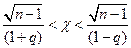
Вероятность этого неравенства и неравенство ( ) равна
) равна
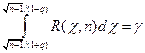
Из этого уравнения можно по заданным n и 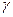 найти q. Практически пользуются таблицей. Вычислив по выборке s и найдя по таблице q, получаем интервал, покрывающий
найти q. Практически пользуются таблицей. Вычислив по выборке s и найдя по таблице q, получаем интервал, покрывающий 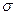 с заданной надежностью
с заданной надежностью 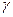
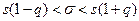 (1 +0,32).
(1 +0,32).
При q > 1 неравенство (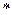 ) примет вид
) примет вид
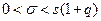
Пример 3. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 25 найдено «исправленное» среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 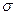 с надежностью
с надежностью 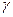 = 0,95.
= 0,95.
Решение. По таблице по данным 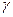 = 0,95 и n = 25 найдем q = 0,32.
= 0,95 и n = 25 найдем q = 0,32.
Искомый доверительный интервал (*) таков: 0,8  (1- 0,32) <
(1- 0,32) < 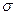 < 0,8
< 0,8  (1+ 0,32)
(1+ 0,32)
или 0,544 < 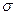 < 1,056. Практически для отыскания значений q > 1, соответствующих различным заданным n и
< 1,056. Практически для отыскания значений q > 1, соответствующих различным заданным n и 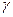 , пользуются той же таблицей.
, пользуются той же таблицей.
Пример 4. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=10 найдено «исправленное» среднее квадратическое отклонение s = 0,16. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 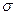 с надежностью 0,999.
с надежностью 0,999.
Решение. По таблице по данным 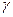 = 0,999 и n =10 найдем q = l,8 (q > 1). Искомый доверительный интервал таков:
= 0,999 и n =10 найдем q = l,8 (q > 1). Искомый доверительный интервал таков:
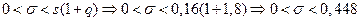 .
.
 2015-07-21
2015-07-21 9194
9194








