2015-07-21
896
Каждой квадратной матрице поставим в соответствие число, которое назовем ее определителем или детерминантом и будем обозначать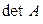 
, следующим образом:
а) если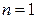 
, то 
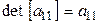(определитель матрицы, состоящей из одного элемента, равен этому элементу);
б) если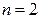 
, то
;
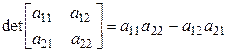в) если известно, как найти определитель матрицы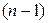 
-го порядка, то определитель матрицы 
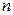-го порядка задается так:
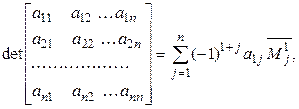(1.10)
где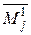 
− определитель матрицы 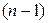-го порядка, полученной из исходной вычеркиванием первой строки и 
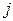-го столбца.
Определитель квадратной матрицы n -го порядка будем просто называть определителем n -го порядка.
В развернутом виде определитель n -го порядка записывается как таблица, ограниченная с обеих сторон вертикальными чертами (по одной с каждой стороны):
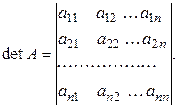
Приведенное выше определение является определением по индукции или определением с помощью разложения по первой строке.
Пусть А – некоторая матрица, не обязательно квадратная. Выделим в ней k строк и k столбцов. Элементы, расположенные на пересечениях выделенных строк и столбцов, образуют определитель k -гo порядка, который называется минором k -гo порядка матрицы А (или определителя) и обозначается
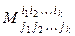, (1.11)
где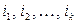 
– номера выделенных строк, 
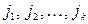– номера выделенных столбцов.
Если А – квадратная матрица n -го порядка (или определитель), то элементы, оставшиеся после вычеркивания выделенных строк и столбцов, также образуют определитель порядка n – k. Его называют минором, дополнительным к минору (1.11), и обозначают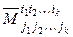 
. Алгебраическим дополнением к минору (1.11) называется число
.
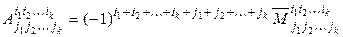Очевидно, алгебраическое дополнение к некоторому минору от дополнительного минора может отличаться разве что знаком. Например, если
,
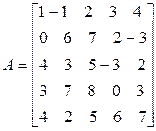то
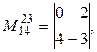
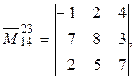
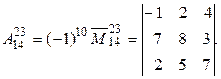
Каждый элемент матрицы А (или определителя) является ее минором первого порядка, и поэтому для него определяется как дополнительный минор, так и алгебраическое дополнение. В алгебраическом дополнении к одному элементу оба индекса станем писать снизу, считая, как обычно, первый индекс номером вычеркиваемой строки, а второй – столбца.
Используя введенные обозначения, равенство (1.10) можно записать так:
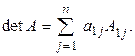
Таким образом, согласно определению, определитель равен сумме произведений элементов первой строки на их алгебраические дополнения.
