Метод Гаусса-Зейделя

В отличие от метода Якоби, в котором вычисления всех компонент вектора 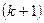-го приближения проводилось однообразно, в методе Гаусса-Зейделя для расчета 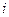-й компоненты следующего приближения используется уже вычисленное на этом, т.е. 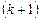-м шаге, новые значения первых 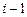компонент:

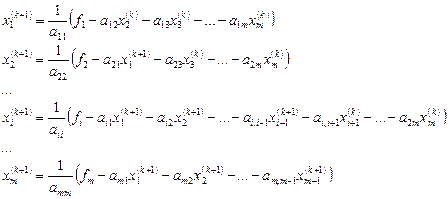Или, в компактном виде:

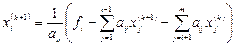, i =1, 2, …, m. (2.12)

Достаточное условие сходимости этого метода, как и для методы Якоби, является условие диагонального преобладания:

, .

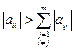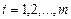ПРИМЕР 2.6. Найдем решение СЛАУ из Примера 2.4 методом Гаусса-Зейделя.

.

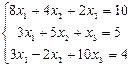Расчетные формулы:

.

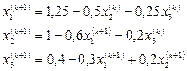Таблица итераций выглядит в данном случае следующим образом:

Номер итерации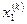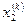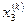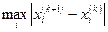
	1.25	0.25	0.075	1.25
	1.10625	0.32125	0.132375	0.14375
	1.056281	0.339756	0.151067	0.049969
	1.042355	0.344374	0.156168	0.013926
	1.038771	0.345504	0.157469	0.003584

Здесь

,

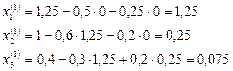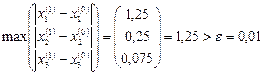
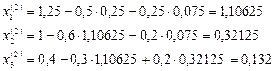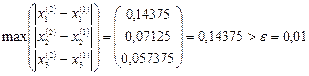, и т.д.

Из таблицы видно, что нужная точность достигнута уже на 5-ой итерации вместо 11-ой по методу простой итерации.

При реализации в Excel расчетные формулы для 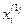примут вид: 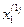=1/$B$1*($G$1-$C$1*C6-$D$1*D6),

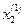=1/$C$2*($G$2-$B$2*B7-$D$2*D6), 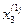=1/$D$3*($G$3-$B$3*B7-$C$3*C7).