2015-07-21
2281
Рассмотрим метод прогонки для СЛАУ вида:
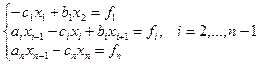(2.6)
Решение данной системы ищем в виде:
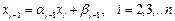(2.7)
Здесь ai, bi – неизвестные прогоночные коэффициенты. Как и метод Гаусса, метод прогонки состоит из двух этапов. На первом (прямом) этапе определяются прогоночные коэффициенты, на втором (обратном) вычисляется вектор решения.
Прямой этап. Сравнивая соотношение (2.7) при i =2: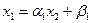 
и следствие первого уравнения системы (2.6): 
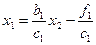, получим формулы для первых прогоночных коэффициентов: 
.
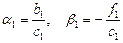Подставляя (2.7) во второе уравнение (2.6), получим:
.
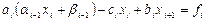Или, после преобразования,
,
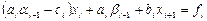откуда
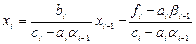
Сравнивая с (2.7), получим
.
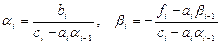Таким образом, можно найти все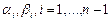 
.
Обратный этап. Подставляя последнее прогоночное соотношение (2.7) в последнее уравнение (2.6), получим:
.
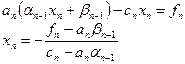Затем, последовательно применяя (2.7), находим:
.
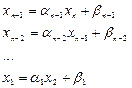Таким образом, алгоритм метода прогонки можно представить в виде:
1. Находим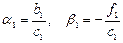 
;
2. Для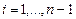 
вычисляем
.
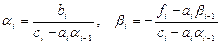3. Находим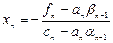 
.
4. Для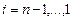 
находим: 
.
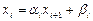Теорема. Пусть коэффициенты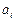 
, 
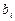системы уравнений при 
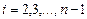отличны от нуля и пусть 
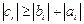при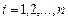 
. Тогда прогонка корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге расчетов, не будет возрастать при переходе к следующим шагам. Данное условие есть не что иное, как условие диагонального преобладания.
