2015-07-21
578
Преобразуем исходную систему линейных уравнений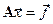 
к эквивалентной системе вида:
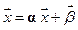, (2.8)
где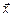 
– искомый вектор, а 
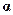и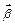 
– некоторые новые матрица и вектор, соответственно. Будем решать (2.8) методом последовательных приближений. В качестве нулевого приближения можно взять 
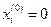. Следующее приближение находим по рекуррентным формулам
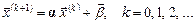(2.9)
Такой итерационный процесс будем называть методом простых итераций (МПИ). Так же, как и в случае МПИ для решения нелинейных алгебраических уравнений, метод (2.9) сходится не для любой матрицы 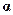. Достаточным условием сходимости МПИ (2.9) к решению системы (2.8) при любом начальном векторе 
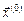является требование 
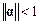, где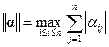 
– норма матрицы .
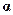Существует несколько способов построения порождающей матрицы 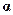, для которой выполняется достаточное условие сходимости.
