Метод Якоби

Предположим, что диагональные элементы матрицы 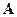исходной системы не равны нулю (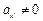, 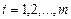). Разрешим первое уравнение системы относительно 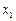, второе относительно 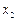и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

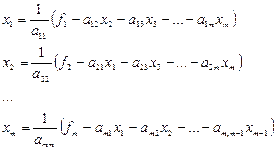. (2.10)

Зададим вектор нулевого приближения 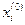. Следующие приближение будем вычислять по рекуррентным соотношениям

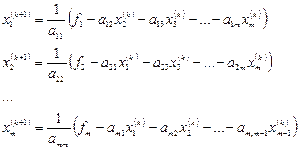(2.11)

В свернутом виде данную систему можно переписать как

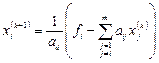, i =1, 2, …, m.

Условием окончания итерационного процесса служит условие .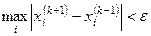

Достаточное условие сходимости. Метод Якоби является вариантом МПИ, в котором

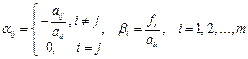
Если для исходной матрицы A выполнено условие диагонального преобладания, т.е. 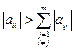, , 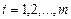то выполняется условие 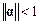, т.е. итерационный процесс (2.11) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием. Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Чаще всего в качестве начального приближения берут 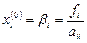или .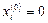

Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Но данное условие не является необходимым, процесс может сходиться и при отсутствии диагонального преобладания.

ПРИМЕР 2.5. Решить СЛАУ из Примера 2.3 с помощью метода Якоби с точностью .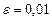

С помощью прямого метода обратной матрицы найдено решение , , .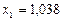

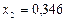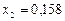Найдем решение методом Якоби. Для начала проверим условие диагонального преобладания:

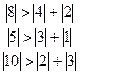
Приводим систему уравнений к виду (2.8):

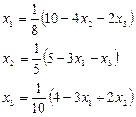или .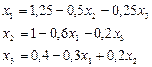

Тогда

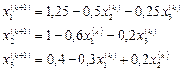
В качестве начального приближения выберем 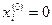. Дальнейшие вычисления оформим в виде таблицы:

Номер итерации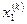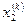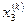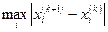
				-
	1.25		0.4	1.25
	0.65	0.17	0.225	0.83
	1.10875	0.565	0.239	0.45875
	0.90775	0.28695	0.180375	0.27805
	1.061431	0.419275	0.185065	0.153681
	0.994096	0.326128	0.165426	0.093147
	1.045579	0.370457	0.166997	0.051483
	1.023022	0.339253	0.160418	0.031204
	1.040269	0.354103	0.160944	0.017247
	1.032712	0.34365	0.15874	0.010453
	1.03849	0.348625	0.158916	0.005778

Здесь , ,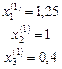

, ,

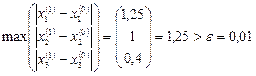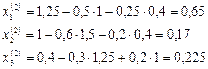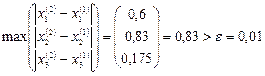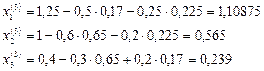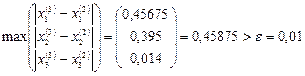, , и т.д.

Процесс продолжается, пока погрешность не станет меньше 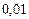, что происходит на 11-ой итерации. Следовательно, приближенное решение имеет вид: 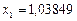, , 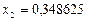, 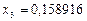что с точностью e совпадает с решением, полученным по методу обратной матрицы.

При реализации в Excel расчетные формулы для 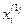, при условии, что исходные данные введены в лист Excel, как показано ниже,

	A	B	C	D	E	F	G
	A=					f=
			-2
	номер итерации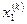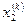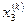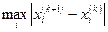
					-
		1.25		0.4	1.25

имеют вид:

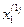=1/$B$1*($G$1-$C$1*C6-$D$1*D6),

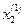=1/$C$2*($G$2-$B$2*B6-$D$2*D6), 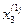=1/$D$3*($G$3-$B$3*B6-$C$3*C6),

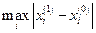{=МАКС(ABS(B8:D8-B7:D7))}.

Фигурные скобки означают нажатие комбинации клавиш ctrl+shift+enter после набора формулы. Остальные формулы для вычисления 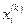получаются копированием.

Можно провести вычисления в табличном процессоре Excel и с использованием функций умножения матрицы на вектор на основе матричной формы (2.9) метода Якоби.

Здесь a= 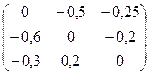, b= .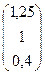

Занесем исходные данные на рабочий лист.

	A	B	C	D	E	F	G
			-0,5	-0,25			1,25
	a =	-0,6		-0,2		b =
		-0,3	0,2				0,4
	номер итерации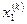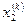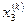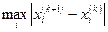
					-
		1.25		0.4	1.25

Выделим ячейки B7:D7 и введем формулу (2.9):

{=МУМНОЖ($B$1:$D$3;ТРАНСП(B6:D6))+ТРАНСП($G$1:$G$3)}.

Остальные формулы для вычисления 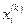получаются копированием.