2015-07-21
2652
Рассмотрим параллельный колебательный контур, простейшим видом которого является параллельное соединение индуктивной катушки и конденсатора (рисунок 29).
Резонансом токов называют такой режим параллельного колебательного контура, при котором ток в неразветвленной части цепи совпадает по фазе с напряжением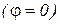 
, а мощность, потребляемая из сети, равна активной мощности контура. Реактивная мощность при резонансе из сети не потребляется.
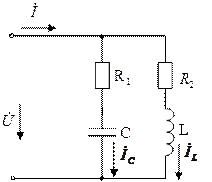
Рисунок 29 – Параллельный колебательный контур
При резонансе токов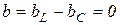 
. При резонансе токов возможны ситуации, когда реактивные ток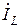и 
и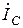 
намного превышают суммарный ток суммарный ток в цепи, вследствие, чего резонанс при параллельном соединении называют резонансом токов. Это возможно при условии 
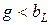или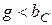 
.
Определим резонансную частоту контура:
.
После преобразования получаем
,
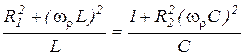откуда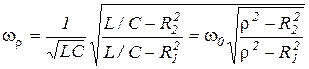 
, где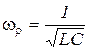 
; 
.
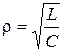Как видно из выражения для резонансной частоты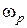 
, резонанс токов возможен при одновременном выполнении условий 
, 
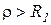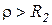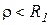или 
и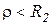 
. Если эти условия не выполняются, то 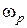− линейное число. В случае, когда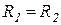 
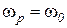при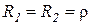 
; 
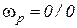, т. е. резонанс токов наступает при любой частоте источника. При этом эквивалентное сопротивление контура не зависит от частоты.
|
|
|
,
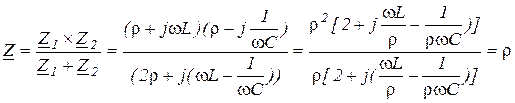где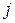 
− комплексное число.
Следовательно, ток в неразветвленной части цепи не зависит от частоты. Есл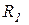и 
и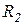 
− сопротивления, учитывающие потери реальных конденсаторов и индуктивной катушки (
; 
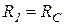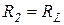), то как правило, 
, 
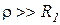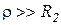при этом 
.
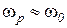В контуре без потерь (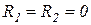
), 
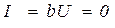, ток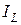и 
и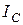 
равны по величине и противоположны по фазе. Эквивалентные сопротивления контура с потерями
,
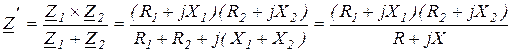где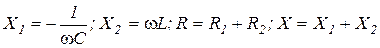 
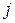; − комплексное число.
В идеальном случае, например в радиотехнических устройствах, где применяют контуры с малыми потерями, когда практически 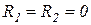(или они очень малы по сравнению с 
), резонансную частоту можно определить, как и при резонансе в последовательном колебательном контуре, по формуле: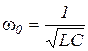 
.
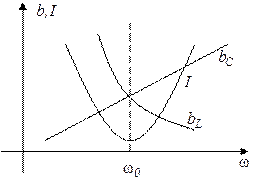Частотные характеристики для резонанса тока изображены на рисунке 30.
Рисунок 30 − Частотные характеристики для резонанса тока
