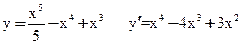Пример 3

приравнивая производную нуль получим 3 стационарные точки x=0 x=1 x=3

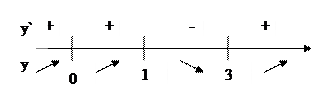x=1 – точка максимума

x=3 – точка минимума

Теорема 2 Второе достаточное условие экстремума.

Пусть 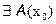функции f(x), где функция определена, непрерывна, существует 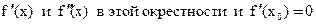. Точка x₀ – стационарная точка.

Тогда

1) Если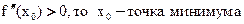

2) Если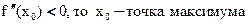

Доказательство:

1) Если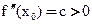

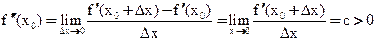(так как 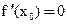по условию)

По определению предела для

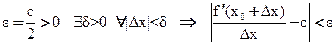
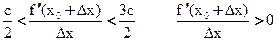
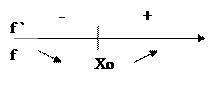
Если ∆x<0 (слева от x₀), то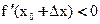

∆x>0, то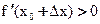

Значит по 1 достаточному условию x₀ – точка минимума. В точке x₀ производная меняет знак с “-” на “+” значит x₀ – точка минимума

2) Для 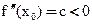доказательство аналогичное

Теорема 3 Третье достаточное условие экстремума.

Пусть такая, что:

1) f(x) определена и непрерывна в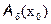

2)

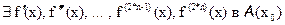
3)

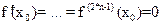
4)

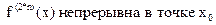
Тогда

1) если 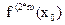>0, то x₀ – точка минимума

2) если 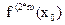<0, то x₀ – точка максимума

Доказательство:

По условию 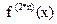и непрерывна в x₀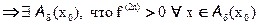

Аналогично теореме 2(предыдущая).

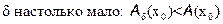
В 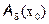разложим функцию по формуле Тейлора:

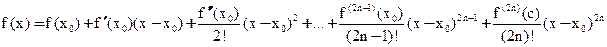
c- промежуточная между x и x₀

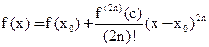, где 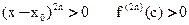значит

f(x)≥f(x₀) x₀ – точка минимума по определению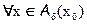

Для 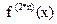=с <0 – аналогично.