Функция называется выпуклой вверх на промежутке X, если её график лежит ниже касательной на этом промежутке.
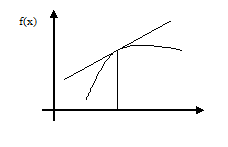
|
f(x) 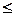 f(x0)+f `(x0)(x-x0),
f(x0)+f `(x0)(x-x0), 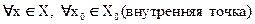
Теорема 1 Первый критерий выпуклости функции на промежутке
Пусть функция f(x) определена и непрерывна на промежутке X, дифференцируема в любой внутренней точке (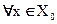 )
)
Тогда:
1) f(x)-выпукла вниз на X 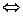 f `(x) – неубывающая на X0
f `(x) – неубывающая на X0
2) f(x)-выпукла вверх на X 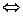 f `(x) – невозрастающая X0
f `(x) – невозрастающая X0
Доказательство:
 1) Необходимость
1) Необходимость
По условию, f(x) выпукла вниз, докажем, что f `(x) неубывающая (то есть 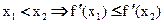 )
)
Возьмём 
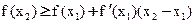 - по определению выпуклости
- по определению выпуклости
 - по определению выпуклости
- по определению выпуклости
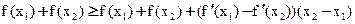
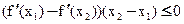 , так как
, так как 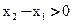

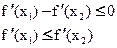
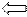 1) Достаточность
1) Достаточность
По условию производная - неубывающая, доказать f(x)-выпукла вниз, то есть 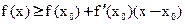
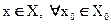 (1)
(1)
Пусть для определённости 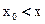
Докажем:
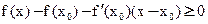 (2)
(2)
На отрезке от x до x0 выполняются условия теоремы Лагранжа
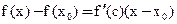 (3)
(3)
подставив (3) в (2)
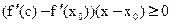
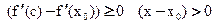
(1) (2) (3) – равносильны
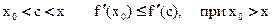 доказательство аналогичное
доказательство аналогичное
2) для пункта 2 аналогично пункту 1

Теорема 2 Второй критерий выпуклости функции на промежутке
Пусть функция f(x) определена и непрерывна на промежутке X и дифференцируема в любой внутренней точке промежутка
Тогда
1) f(x)-выпукла вниз на X 
 (x)
(x) 
2) f(x)-выпукла вверх на X 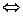
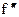 (x)
(x) 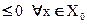
Доказательство:
 Необходимость
Необходимость
f(x) – выпукла вниз на промежутке тогда и только тогда, когда f `(x) 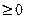 по первому критерию выпуклости
по первому критерию выпуклости
 Достаточность
Достаточность
По критерию монотонности 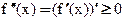
 |
 2015-07-14
2015-07-14 209
209








