Пример 1

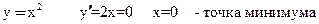
Пример 2

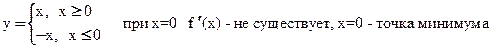
Пример 3

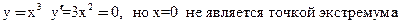
Определение

Если производная в некоторой точке равна нулю, то такая точка называется стационарной

Определение

Если производная в некоторой точке равна нулю или не существует конечная – то такие точки называются критическими

Теорема 1 Первое достаточное условие экстремума.

Пусть 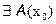функции f(x) такая, что

1) f(x) – определена и непрерывна в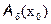

2) дифференцируема в 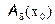, кроме быть может самой точки x₀,

Тогда если

1)

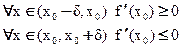
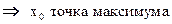
2)

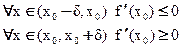
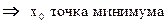
Доказательство:

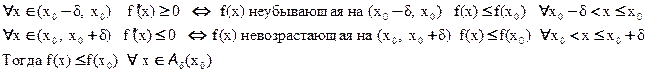это значит, x₀ – точка локального максимума по определению

Пример 1

y=|x| x=0 – критическая точка, так как 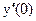не существует

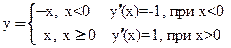
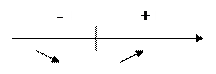, значит x=0 точка минимума

Пример 2

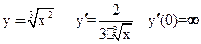x=0 – критическая точка

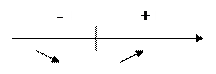, x=0 точка минимума