Определение

x₀ – точка локального максимума, если

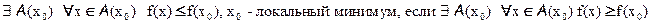
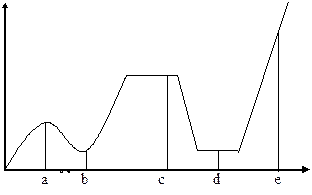
a, с – точки локального максимума

а – строгий локальный максимум

с – нестрогий локальный максимум

(b, d – локальный минимум, b – строгий,

d- нестрогий)

Значения функции в точках максимума(минимума) не обязательно являются наибольшими(наименьшими) значениями функции(наибольшие или наименьшие значение может достигаться на конце отрезка).

Теорема 1 Необходимые условия экстремума

Если x₀ – точка максимума функции f(x) (f(x) – определена и непрерывна в окрестности x₀)

Тогда: либо 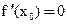, либо 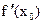не существует конечная.

Доказательство:

В окрестности точки x₀ функция удовлетворяет условиям теоремы Ферма, если 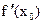- существует конечная, тогда по теореме Ферма 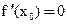. А в остальных случаях 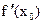не существует.