Пример 3

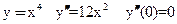
x=0 – не является точкой перегиба

Теорема Первое достаточное условие точки перегиба

Пусть в некоторой окрестности точки x₀ существует 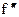(x) в каждой точке, кроме возможно самой точки x₀. Причём в левой части окрестности вторая производная имеет один знак, а в правой другой.

Тогда x₀ – точка перегиба

Доказательство:

Для определённости примем в левой части 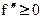(функция выпукла вниз), а в правой 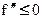(функция выпукла вверх). Тогда в точке x₀ – меняется направление выпуклости, тогда x₀ – точка перегиба по определению

Теорема Второе достаточное условие точки перегиба

Пусть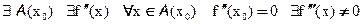

Тогда x₀ – точка перегиба

Доказательство:

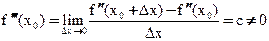
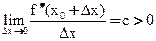
(так как 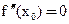по условию)

По определению предела для

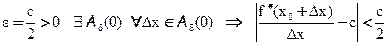
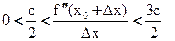
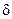настолько мало, ч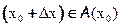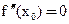то . , то

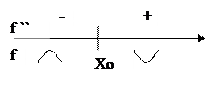
Если ∆x<0 (слева от x₀), то 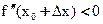, функция выпукла вверх

∆x>0 то 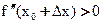, функция выпукла вниз

Значит x₀ – точка перегиба по определению.

Теорема Третье достаточное условие точки перегиба

Пусть в некоторой окрестности точке x₀ – существуют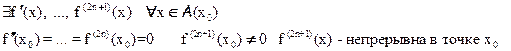

Тогда x₀ – точка перегиба

Доказательство:

Пусть 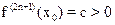тогда в силу непрерывности функции 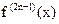в точке x₀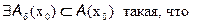 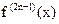>0. В этой 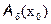разложим функцию в ряд Тейлора.

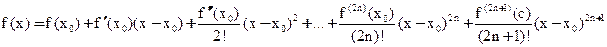
c- промежуточная между x и x₀

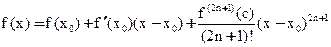, где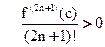

Если x<x₀ – то последнее слагаемое отрицательно

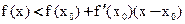
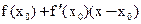- касательная,

Значит f(x) – выпукла вверх при x<x₀

Если x>x₀ – то последнее слагаемое положительно

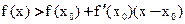
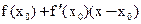- касательная,

Значит f(x) – выпукла вниз при x<x₀

В точке x₀ – меняется направление выпуклости, значит она по определению будет точкой перегиба.