Из колоды в 36 карт наудачу берут одну карту. События: 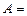 {взят туз},
{взят туз}, 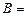 {взята карта бубновой масти}.
{взята карта бубновой масти}.
Найти 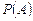 и
и 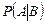 .
.
◄По формуле классической вероятности находим: 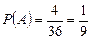 ;
; 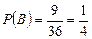 ;
; 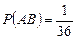 . Поэтому
. Поэтому 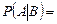
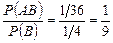 .
.
Итак, 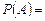
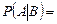
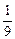 , т.е. условная и безусловная вероятности события
, т.е. условная и безусловная вероятности события  совпадают.►
совпадают.►
Таким образом, наступление события  может влиять или не влиять на вероятность события
может влиять или не влиять на вероятность события  . Поэтому степень связи (зависимости) событий
. Поэтому степень связи (зависимости) событий  и
и  естественно оценивать путём сравнения их условных вероятностей с безусловными.
естественно оценивать путём сравнения их условных вероятностей с безусловными.
Говорят, что событие  не зависит от события
не зависит от события  , если
, если
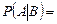
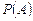 (1.8.1)
(1.8.1)
и наоборот, событие  не зависит от события
не зависит от события  , если
, если
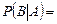
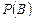 (1.8.2)
(1.8.2)
(предполагается, что 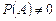 ,
, 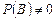 ).
).
Замечания
1. Оказывается, что свойство независимости событий – взаимно, т.е. если событие  не зависит от события
не зависит от события  , то и наоборот: событие
, то и наоборот: событие  не зависит от события
не зависит от события  . Поэтому говорят о взаимной независимости или просто независимости событий
. Поэтому говорят о взаимной независимости или просто независимости событий  и
и  , если выполняется одно из соотношений (1.8.1) или (1.8.2).
, если выполняется одно из соотношений (1.8.1) или (1.8.2).
◄Пусть событие  не зависит от события
не зависит от события  , т.е. выполняется (1.8.2). Тогда с учётом теоремы умножения (3.1.6) получаем:
, т.е. выполняется (1.8.2). Тогда с учётом теоремы умножения (3.1.6) получаем: 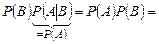
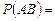
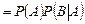 , откуда, после сокращения на
, откуда, после сокращения на 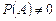 , имеем:
, имеем: 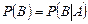 . Это означает, что, событие
. Это означает, что, событие  не зависит от события
не зависит от события  .►
.►
2. Из проведённых только что выкладок следует: если события  и
и  независимы, то
независимы, то
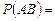
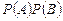 . (1.8.3)
. (1.8.3)
Верно и обратное: из (1.8.3) следует независимость событий  и
и  (убедитесь!). Поэтому используют и эквивалентное определение независимости событий: события
(убедитесь!). Поэтому используют и эквивалентное определение независимости событий: события  и
и  называются независимыми, если
называются независимыми, если 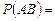
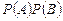 . В этом определении отсутствует требование
. В этом определении отсутствует требование 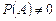 ,
, 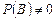 .
.
 2015-07-21
2015-07-21 221
221








