2015-07-21
251
Пусть события 
и 
независимы. Покажем, что тогда независимыми являются и события 
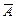и .
◄Условная вероятность обладает всеми свойствами безусловной, поэтому и с учётом (1.8.1) имеем: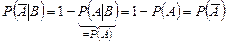 
, что означает независимость событи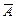й и .►
Упражнения
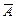1.8.1. Докажите, что если события и независимы, то и события и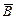 
являются независимыми.
1.8.2. Убедитесь в том, что если и - несовместные события с ненулевыми вероятностями, то они зависимы.
1.8.3. Если события и совместны, то они могут быть и зависимыми и независимыми. Приведите примеры, иллюстрирующие это утверждение.
1.8.4. Если и - зависимые события, то они могут быть и совместными, и несовместными. Проиллюстрируйте это примерами.
Замечание
Как распространить понятие независимости двух событий на набор из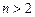 
событий? Смысл независимости двух событий и состоит в том, что появление одного из них не влияет на вероятность другого. Естественно считать независимыми события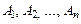 
, если вероятность каждого из этих событий 
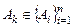не зависит от того какие из остальных событий 
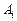и в каком количестве произошли. При этом независимость 
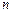событий при 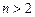называют независимостью в совокупности.
|
|
|
Итак, события 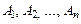, 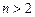называют независимыми в совокупности, если для любого набора 
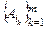из этих событий (
; 
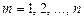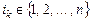) выполняется равенство
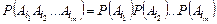. (1.8.4)
В частности, для событий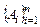 
, независимых в совокупности,
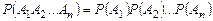. (1.8.5)
Формула (1.8.5) обобщает равенство (1.8.3) и является частным случаем формулы вероятности произведения событий (1.7.7): она соответствует событиям 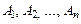, независимым в совокупности.
